Функциональные ряды. Функциональным рядом называется ряд, члены которого являются функциями от

Функциональным рядом называется ряд, члены которого являются функциями от

Зафиксируем некоторое значение получим числовой ряд:

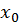Если числовой ряд сходится, то значение называется точкой сходимости функционального ряда Множество всех точек сходимости функционального ряда называется областью его сходимости. Если числовой ряд расходится, то называется точкой расходимости функционального ряда

Функциональный ряд называется абсолютно сходящимся в некоторой области, если в ней сходится ряд из модулей его членов:

Поскольку каждой точке 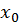сходимости ряда ставится в соответствие определенное значение суммы ряда , то сумма сходящегося в некоторой области функционального ряда является функцией переменной 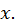Обозначим эту функцию через тогда

где - я частичная сумма ряда т.е.

Остатком функционального ряда после - го члена называется ряд, полученный из данного отбрасыванием его первых членов. Отметим, что функциональный ряд и любой его остаток в некоторой области одновременно сходятся или расходятся.

Пусть функциональный ряд сходится в некоторой области. Сумму остатка после - го члена обозначим через Тогда

Отсюда следует, что

Важным частным случаем функциональных рядов являются степенные ряды.

Поиск по сайту: