АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Частные и полное приращения функции нескольких переменных

Читайте также:
  1. II. Основные задачи и функции
  2. II. Разделы социологии: частные социальные науки
  3. III. Предмет, метод и функции философии.
  4. IV. Конструкция бент-функции
  5. Ms Excel: мастер функций. Логические функции.
  6. Public void тестОтчетаНесколькихПосещений()
  7. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  8. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  9. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  10. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  11. V2: Функции исторической науки
  12. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ

Рассмотрим линию 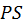пересечения поверхности с плоскостью параллельной плоскости Так как в этой плоскости сохраняет постоянное значение, то 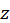вдоль кривой 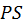будет меняться только в зависимости от изменения Дадим независимой переменной приращение тогда 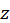получит приращение, которое называют частным приращением 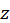по и обозначают через так что

Аналогично, если сохраняет постоянное значение, а получает приращение то 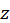получает приращение, называемое частным приращением 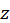по 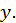Это приращение обозначают символом

Приращение функция получает вдоль линии пересечения поверхности с плоскостью 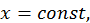параллельной плоскости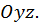

Наконец, сообщив аргументу приращение 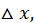а аргументу приращение получим для 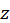новое приращение которое называется полным приращением функции 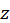и определяется формулой:

Отметим, что, вообще говоря, полное приращение не равно сумме частных приращений.

Аналогичным образом определяются частные и полное приращения функции любого числа переменных. Так для функции трех переменных имеем:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

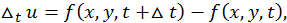
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)