Теорема о необходимом признаке возрастания (убывания) функции

1) Если дифференцируемая функция возрастает на некотором промежутке, то производная этой функции неотрицательна на этом промежутке, т.е.

2) Если дифференцируемая функция убывает на некотором промежутке, то ее производная не положительна на этом промежутке; т.е.

Доказательство. 1) Пусть дифференцируемая функция возрастает на 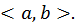Согласно определению производной Если значения то в силу возрастания функции 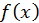знак ее приращения где одинаков со знаком приращения аргумента 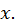Следовательно, при достаточно малом по абсолютной величине имеем: Переходя в последнем неравенстве к пределу при и учитывая, что предел положительной функции, очевидно, не может быть отрицательным, получим

2) Доказательство второй части теоремы аналогично доказательству первой части (провести самим!).

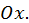Замечание. Геометрически утверждение теоремы сводится к тому, что для графика возрастающей дифференцируемой функции касательные образуют с положительным направлением оси острые углы α или в некоторых точках параллельны оси Для графика убывающей дифференцируемой функции все касательные образуют тупые углы с положительным направлением оси или параллельны ей.

Поиск по сайту: