Вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона применяется для интерполирования в окрестности конечного значения .

Пусть для функции 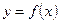заданы значения для равноотстоящих значений независимой переменной . Построим полином следующего вида:

. (5.29)

Используя обобщенную степень, получим:

. (5.30)

Найдем коэффициенты из условий . Эти условия равносильны

. (5.31)

Полагая в выражении (5.30), получим

. (5.32)

Чтобы найти коэффициент 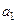, составим первую конечную разность:

.

Полагая , получим:

.

Отсюда

. (5.33)

Из второй конечной разности

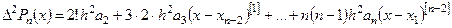
при находим:

.

Следовательно,

. (5.34)

Продолжая дальнейшее вычисление конечных разностей, получим:

. (5.35)

Подставляя найденные значения коэффициентов 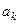в выражение (5.29), получим вторую интерполяционную формулу Ньютона:

(5.36)

Введем новую переменную

, (5.37)

тогда

(5.38)

С учетом (5.38) вторая интерполяционная формула Ньютона примет вид:

. (5.39)

Остаточный член второй интерполяционной формулы Ньютона:

, (5.40)

где 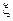- промежуточное значение между узлами интерполирования и точкой .

Поиск по сайту: