Постановка задачи аппроксимации и интерполяции функций

Лекция 5.

Методы приближения ФУНКЦИЙ.

Постановка задачи аппроксимации и интерполяции функций.

В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функции.

Поводом для аппроксимации функции может послужить, в частности, табличный способ ее задания. Предположим, что в результате некоторого эксперимента для конечного набора значений 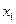величины из отрезка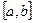

получен набор значений величины 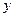. Если допустить, что между и 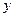существует функциональная зависимость , можно поставить вопрос о поиске аналитического представления функции .

Повод для аппроксимации может возникнуть даже тогда, когда аналитическое выражение некоторой функции имеется, однако оно оказывается мало пригодным для решения поставленной задачи, потому что операция, которую требуется осуществить над этой функцией, трудновыполнима или невыполнима совсем. Например, вычисление значения трансцендентной функции «вручную». Действительно, чтобы вычислить проще всего воспользоваться степенным разложением функции, т.е. заменить трансцендентную функцию степенным рядом. При этом получается приближенное значение функции.

Другая ситуация, когда может потребоваться аппроксимация аналитически заданной функции – дифференцирование функции, вычисление определенных и неопределенных интегралов. Если аналитическое выражение функции достаточно сложное, то поставленная задача трудно выполнима, а иногда и невыполнима с помощью элементарных приемов. Например, интеграл 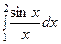существует, но по формуле Ньютона-Лейбница практически вычислен быть не может, т.к. первообразная не выражается в элементарных функциях. Аппроксимация подынтегральной функции – один из возможных приемов.

Классический подход к численному решению подобных задач заключается в том, чтобы, опираясь на информацию о функции , по некоторому алгоритму подобрать аппроксимирующую функцию , в определенном смысле «близкую» к .

Для оценки «близости» функций выбирают тот или иной критерий согласия. Эти критерии основаны на использовании той или иной метрики, т.е. способа введения расстояния между функциями, принадлежащими тому или иному классу: . Например, для функций, ограниченных на отрезке 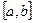, расстояние может быть введено следующим образом: ; для функций, непрерывных на отрезке 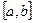, по формуле .

Часто процедура аппроксимации связана с другим критерием согласия:

.

Применяемый на его основе способ аппроксимации получил название метода наименьших квадратов.

Для функций, заданных таблично, достаточно распространенным критерием согласия является критерий Чебышева, который определяет расстояние между аппроксимируемой и аппроксимирующей функциями как максимум величины отклонения между этими функциями в узлах сетки:

.

Если , т.е. , то соответствующий способ аппроксимации называют интерполяцией, а процедуру вычисления значений с помощью в точках, не являющихся узлами сетки - интерполированием.

Задача интерполирования состоит в следующем.

На отрезке 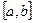заданы точки , которые называются узлами интерполяции, и значения некоторой функции в этих точках:

. (5.1)

Необходимо построить функцию - интерполирующую функцию, принадлежащую некоторому классу и принимающую в узлах интерполяции заданные значения (5.1), т.е.

. (5.2)

Геометрически это означает, что нужно найти кривую определенного типа, проходящую через заданные точки .

В такой общей постановке задача может иметь бесконечное множество решений или совсем их не иметь.

Сформулированная задача становится однозначной, если вместо произвольной функции искать полином степени не выше , удовлетворяющего условиям (5.2), т.е.

.

Полученную интерполяционную функцию используют для приближенного вычисления значений данной функции в точках, отличных от узлов интерполяции. Такая операция называется интерполированием функции.

Различают интерполирование в узком смысле, т.е. когда , и экстраполирование, т.е. когда . В дальнейшем, под термином интерполирование будет пониматься как первая, так и вторая операции.

Поиск по сайту: