Конечные разности. Обобщенная степень

Пусть задана функция . Обозначим через фиксированную величину приращения аргумента (шаг). Тогда выражение

(5.3)

называется первой конечной разностью функции . Аналогично определяются конечные разности высших порядков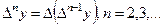

Например:

(5.4)

Символ (дельта) можно рассматривать как оператор, ставящий в соответствие функции функцию .

Легко проверить основные свойства оператора :

1) ;

2) ;

3) 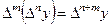, где (целые неотрицательные числа), причем .

Из формулы (5.3) имеем:

.

Отсюда, рассматривая как символический множитель, получим:

. (5.5)

Из формулы (5.4):

; (5.6)

и т.д. Окончательно получим:

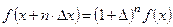. (5.7)

В дальнейшем нам понадобится понятие обобщенной степени.

Поиск по сайту: