Первая интерполяционная формула Ньютона

Пусть для функции 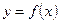заданы значения для равноотстоящих значений независимой переменной , где - шаг интерполяции. Требуется подобрать полином 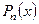степени не выше , принимающий в точках 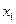значения

. (5.13)

Условия (5.13) эквивалентны тому, что

. (5.14)

Будем искать полином в виде

. (5.15)

Используя понятие обобщенной степени, запишем выражение (5.15) в виде:

. (5.16)

Чтобы полином был определен, нужно найти коэффициенты 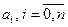. Полагая в выражении (5.16), получим

. (5.17)

Чтобы найти коэффициент 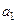, составим первую конечную разность:

.

Полагая , получим:

,

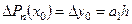откуда

. (5.18)

Для определения коэффициента составим вторую конечную разность:

.

Положив , получим:

,

откуда

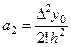. (5.19)

Продолжая процесс, получим:

, (5.20)

причем .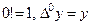

Подставляя найденные значения коэффициентов 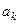в выражение (5.16), получим интерполяционный полином Ньютона:

. (5.21)

Этот полином полностью удовлетворяет требованиям поставленной задачи. Действительно, степень полинома 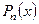не выше ; ;

Для практического использования первую интерполяционную формулу Ньютона записывают в несколько преобразованном виде. Для этого введем новую переменную

. (5.22)

Тогда

(5.23)

Подставляя (5.23) в (5.21), получим окончательный вид первой интерполяционной формулы Ньютона:

. (5.24)

Если в формуле (5.24) положить 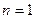, то получим формулу линейного интерполирования:

. (5.25)

При 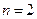получим формулу параболического или квадратичного интерполирования:

. (5.26)

Первую интерполяционную формулу Ньютона используют для интерполирования функции в окрестности начальной точки , где мало по абсолютной величине и представляет собой число шагов, необходимых для достижения точки , исходя из точки .

Остаточный член первой интерполяционной формулы Ньютона:

, (5.27)

где 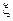- некоторое промежуточное значение между узлами интерполирования и рассматриваемой точкой .

Учитывая, что , приближенно можно положить:

.

В этом случае соотношение (5.27) примет вид:

. (5.28)

Поиск по сайту: