АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод наименьших квадратов для обработки результатов экспериментов

Читайте также:
  1. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Методические основы оценки эффективности инвестиционных проектов
  5. I. Предмет и метод теоретической экономики
  6. I. Что изучает экономика. Предмет и метод экономики.
  7. II. Метод упреждающего вписывания
  8. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  9. II. Методы непрямого остеосинтеза.
  10. II. Проблема источника и метода познания.
  11. II. Рыночные методы.
  12. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ

 

Данный метод относится к классу аппроксимационных методов. Идея метода состоит в том, чтобы по данным эксперимента построить приближенно функцию, отображающую зависимость ее от , в виде многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна. Будем строить функцию в виде многочлена

.

Используем для построения результаты эксперимента:

Таблица 5.3

…
…

 

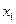
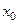
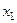
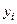
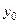
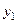
Построить многочлен, значит, определить его коэффициенты . Для этого введем функцию и потребуем, чтобы , где - отклонение функции от экспериментальной в узлах .

Используя вид , получим:

.

Необходимыми условиями экстремума функции 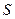является равенство нулю ее первой производной по всем переменным . Расписав эти условия, получим СЛАУ вида:

Запишем систему для определения в нормальной форме:

Решим систему одним из известных методов и найдем коэффициенты , которые затем подставим в искомый многочлен.

Запишем алгоритм метода наименьших квадратов.

1. Вводим таблицу чисел .

2. Вычисляем , .

3. Решая любым известным методом полученную систему линейных алгебраических уравнений, находим - коэффициенты искомого многочлена.

Пример 5.2. По заданной системе точек (см. Табл.5.3) из примера 5.1 построить аппроксимационные многочлены первого и второго порядков методом наименьших квадратов.

Для построения необходимо вычислить следующие суммы

,

и решить СЛАУ относительно неизвестных коэффициентов вида:

Значения неизвестных коэффициентов равны:

Тогда искомый многочлен первого порядка будет иметь вид:

.

Погрешность вычислений по данной формуле в контрольной точке составляет

.

Для построения многочлена второго порядка дополнительно необходимо вычислить следующие суммы

,

и решить СЛАУ относительно неизвестных коэффициентов вида:

Значения неизвестных коэффициентов равны:

.

Тогда искомый многочлен второго порядка будет иметь вид:

.

Нетрудно заметить, что в узловых точках значения многочлена и табличной функции не совпадают (Рис.5.2). Погрешность вычислений по данной формуле в контрольной точке равна:

 
 

.

Рис.5.2.


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)