 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Интерполяционная формула Лагранжа
Пусть на отрезке 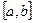 задана произвольная система точек
задана произвольная система точек 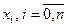 , в которых известны значения функции
, в которых известны значения функции  . То есть, задана следующая таблица
. То есть, задана следующая таблица
Таблица 5.1.
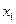
| 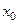
| 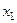
| … | 
|
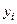
| 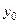
| 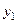
| … | 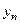
|
Установим зависимость 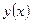 одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.
одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.
Построим многочлен 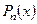 таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть
таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть
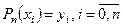 . (5.41)
. (5.41)
Лагранж предложил строить многочлен  -й степени в виде:
-й степени в виде:
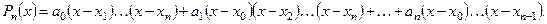 (5.42)
(5.42)
Здесь в каждом слагаемом отсутствует скобка  , которой соответствует коэффициент
, которой соответствует коэффициент  .
.
Найдем неизвестные коэффициенты 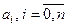 , называемые коэффициентами Лагранжа, используя условие (5.40).
, называемые коэффициентами Лагранжа, используя условие (5.40).
При 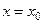 :
: 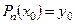 .
.
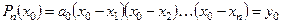 .
.
Следовательно, коэффициент  вычисляется по следующей формуле:
вычисляется по следующей формуле:
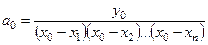 .
.
При  :
: 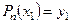 .
.
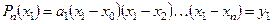 .
.
Следовательно, коэффициент 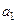 вычисляется по следующей формуле:
вычисляется по следующей формуле:
 .
.
Таким образом, коэффициенты  вычисляются по формулам:
вычисляются по формулам:
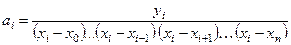 .
.
С учетом найденных коэффициентов интерполяционный полином Лагранжа запишется в виде
 . (5.43)
. (5.43)
Для интерполяционной формулы Лагранжа справедлива оценка погрешности:
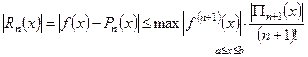 , (5.44)
, (5.44)
где  .
.
Пример 5.1. По заданной системе точек
Таблица 5.2.
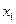
| 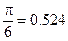
| 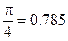
| 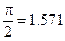
|
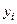
| 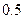
| 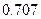
| 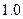
|
построить интерполяционный многочлен Лагранжа второго порядка вида:
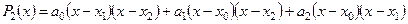 .
.
Коэффициенты этого многочлена будут вычислены по следующим формулам:
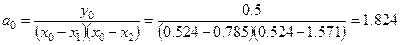 ,
,
 ,
,
 .
.
Тогда многочлен Лагранжа второго порядка будет иметь вид:
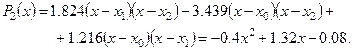
Учитывая, что таблица приведена для функции 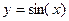 , вычисленной в узловых точках
, вычисленной в узловых точках  , сравним погрешность вычислений данной функции и построенного многочлена в контрольной точке
, сравним погрешность вычислений данной функции и построенного многочлена в контрольной точке 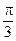 :
:
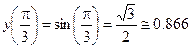 и
и  .
.
Погрешность вычислений равна
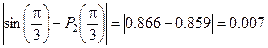 .
.
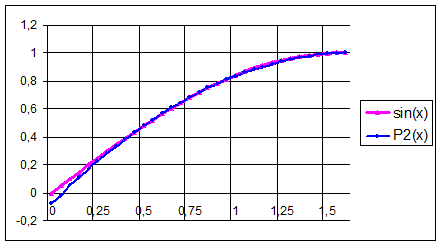 |
Ниже приведены графики функции
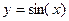 и построенного полинома Лагранжа на заданном интервале. Из рисунка 5.1 видно, что многочлена второго порядка достаточно для обеспечения необходимой точности воспроизводимой синусоиды.
и построенного полинома Лагранжа на заданном интервале. Из рисунка 5.1 видно, что многочлена второго порядка достаточно для обеспечения необходимой точности воспроизводимой синусоиды.
Рис.5.1.
Если таблица 5.1, для которой построена формула Лагранжа, задана для равноотстоящих узлов 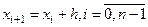 , то формула Лагранжа упрощается. Обозначим через
, то формула Лагранжа упрощается. Обозначим через  . Тогда
. Тогда
 ,
,
 ,…,
,…,
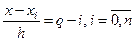 .
.
С учетом введенных обозначений формула Лагранжа запишется так:
 .
.
Запишем формулу Лагранжа в случае, если  :
:
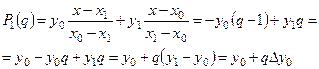 .
.
Получили формулу линейной интерполяции (5.25):
 .
.
Здесь  - табличные разности первого порядка.
- табличные разности первого порядка.
При  получаем формулу квадратичной интерполяции (5.26):
получаем формулу квадратичной интерполяции (5.26):
 .
.
Здесь 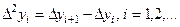 - табличные разности второго порядка, и так далее. Продолжая этот процесс, окончательно получим:
- табличные разности второго порядка, и так далее. Продолжая этот процесс, окончательно получим:
 .
.
Эта формула называется первой интерполяционной формулой Ньютона (сравните с формулой (5.24)). Для нее справедлива оценка остаточного члена (5.27).
Если обозначить через 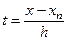 , то с учетом введенного обозначения, получим:
, то с учетом введенного обозначения, получим:
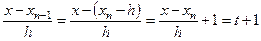 , …,
, …,
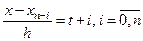 .
.
Тогда формула (5.43) примет вид:
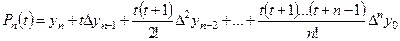 .
.
Эта формула называется второй интерполяционной формулой Ньютона (сравните с формулой (5.39)). Для нее справедлива оценка остаточного члена (5.40).
Поиск по сайту: