Газ в поле тяготения. Барометрическая формула и распределение Больцмана

В основном уравнении МКТ, распределении Максвелла предполагалось отсутствие внешних сил, в то время как молекулы находятся в потенциальном поле тяготения Земли. Найдем зависимость давления от высоты .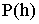

Выделим в атмосфере вертикальный столб с постоянным сечением (рис. 6). Пусть температура 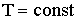, поле тяготения однородно. На высоте давление 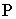связано с весом воздуха, находящемся от до границы атмосферы. Из условия равновесия

,

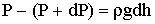где - плотность на высоте .

При давлениях, близких к нормальным, воздух можно рассматривать как идеальный газ

(из уравнения состояния идеального газа),

Для слоя воздуха с параметрами от () до ()

,

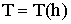- в общем случае.

Для изотермической атмосферы ()

- барометрическая формула.

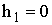Относительно уровня моря, где равно нормальному давлению и , зависимость давления от высоты имеет вид

.

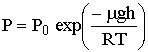Из формулы находится 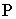по или по 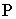. Прибор для измерения высоты, основанный на этой зависимости, – высотомер (альтиметр).

( и 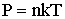) или (, ):

,

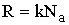где , - число молекул в единице объема на высоте и .

Эта формула описывает распределение молекул по высоте; здесь числитель отражает притяжение молекул к Земле, а знаменатель отвечает за их тепловое движение, разбрасывающее молекулы по всем высотам.

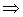
- распределение Больцмана.

Для одинаковых частиц, находящихся в состоянии теплового равновесия, формула может быть использована для любого потенциального силового поля (не только поля сил тяжести).

Поиск по сайту: