АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение политропического процесса, уравнение Пуассона

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. V2: Волны. Уравнение волны
  3. V2: Уравнение Шредингера
  4. Адиабата Пуассона
  5. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. Великое переселение народов: сущность процесса, причины, хронология.
  10. Влияние параметров настройки регулятора на форму переходного процесса, т.е. на показатели качества регулирования
  11. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  12. Волна вероятности. Уравнение Шредингера

Политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость С газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.

Для идеального газа уравнение политропы может быть записано в виде: или .

где величина называется показателем политропы, где .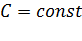

В зависимости от процесса можно определить значение n:

1. Изотермический процесс: n = 1, так как PV 1 = const, значит PV = const, значит T = const.

2. Изобарный процесс: n = 0, так как PV 0 = P = const.

3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона. Здесь γ — показатель адиабаты.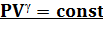

1атомный 2атомный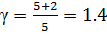

4. Изохорный процесс: , так как , значит P 1 / P 2 = (V 2 / V 1) n, значит V 2 / V 1 = (P 1 / P 2)(1 / n ), значит, чтобы V 2 / V 1 обратились в 1, n должна быть бесконечность.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)