 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
А. Постановка транспортной задачи
Симплексный метод – наиболее универсальный для решения задач линейного программирования, но в практическом применении мы сталкиваемся со значительными трудностями. Существуют классы задач, которые могут быть решены методами, требующими менее сложного алгоритма решения. Наиболее широким классом таких задач являются так называемые транспортные задачи, с которыми приходится встречаться в хозяйственной деятельности.
Сформулируем транспортную задачу в общем виде:
В m пунктах производства 
находится однородный груз (уголь, картофель и т.д.) в количествах соответственно 
ед., который должен быть доставлен n потребителям 
в количествах 
ед. Известны транспортные издержки 
(расходы), связанные с перевозкой единицы груза из пункта 
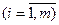в пункт 
. Требуется составить такой план перевозок, который обеспечивал бы при минимальных транспортных издержках удовлетворение спроса всех пунктов потребления за счет распределения всего груза, произведенного всеми пунктами поставки.
Для разрешимости поставленной задачи необходимо и достаточно, чтобы сумма запасов груза равнялась сумме спроса на него, т.е.
(1)
Такую транспортную задачу называют закрытой или задачей с правильным балансом, если же условие (1) нарушается, то – открытой. На практике условие (1), как правило, не выполняется.
Поэтому надо знать, как открытую задачу нормально привести к закрытой. (Что необходимо и достаточно для разрешимости транспортной задачи?)
Если суммарный запас груза превышает общий спрос, т.е. (Как изменится равенство (1)?)
то (Как вы думаете, что нужно сделать?) вводится фиктивный (n+1) й пункт потребления 
со спросом, равным небалансу, т.е. (Чему равно bn+1?)
и одинаковыми тарифами обычно равными нулю. Теперь условие разрешимости выполняется, а величина целевой функции остается прежней, (Почему?) т.к. тарифы на дополнительные перевозки равны нулю. При этом грузы, которые должны быть перевезены в пункт фактически останутся в пункте отправления.
Если же общий спрос потребителей больше суммарного запаса груза, т.е. (описать, что делаем)
то вводится фиктивный (m+1) й пункт отправления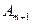 
с запасом груза
Для наглядности поместим все данные сформулированной задачи в таблицу, которую будем называть распределительной или транспортной:
| Поставщик (запас груза) | Потребитель (потребность в грузе) | |||
 ( )
|  ( )
| … |  ( )
| |
 ( )
| 
| 
| … | 
|
 ( )
| 
| 
| … | 
|
| … | … | … | … | .. |
 ( )
| 
| 
| … | 
|
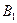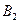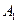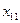
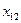
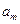Матрицу 
называют матрицей тарифов, а числа - тарифами.
Планом транспортной задачи называют матрицу 
. Её ещё называют матрицей перевозок.
Поиск по сайту: