 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Б. Математическая модель транспортной задачи
Составим математическую модель транспортной задачи.
(Из чего состоит математическая модель общей задачи ЛП?)
(Давайте запишем целевую функцию транспортной задачи?)
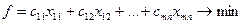 (2)
(2)
(Что можно сказать про переменные? Каким ограничениям они будут удовлетворять?)
Переменные должны удовлетворять ограничениям по запасам:
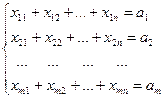 (3)
(3)
ограничениям по потребностям
 (4)
(4)
и условию неотрицательности
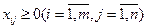 (5)
(5)
Пример: В резерве железнодорожных станций A1,A2 и A3 находится соответственно 100, 150 и 50 порожних вагонов, пригородных для перевозки зерна. Зерно находится в четырех пунктах, которым требуется 75, 80, 60 и 85 вагонов соответственно. Стоимость перегона одного вагона со станции А1 в указанные пункты составляет 6, 7, 3 и 5 ден. ед., со станции A2 - 1, 2, 5 и 6 ден. ед., со станции A3 - 3, 10, 20 и 1 ден. ед. соответственно. Составить экономико-математическую модель задачи, пользуясь которой, можно найти вариант перегона вагонов со станций в пункты погрузки зерна, при котором общие затраты минимизируются.
Составим транспортную таблицу задачи (Учащиеся пытаются составить транспортную таблицу самостоятельно):
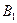 (75) (75)
| 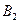 (80) (80)
|  (60) (60)
| 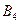 (85) (85)
| |
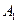 (100) (100)
|
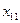
|
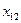
|
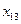
|
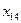
|
 (150) (150)
|

|

|

|
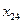
|
 (50) (50)
|

|
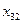
|
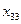
|
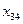
|
Составим математическую модель данной задачи (Учащиеся пытаются составить математическую модель задачи самостоятельно):
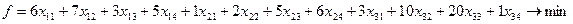
Переменные должны удовлетворять ограничениям по запасам:
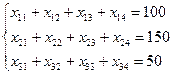
ограничениям по потребностям:

По смыслу переменных, они должны выражаться неотрицательными числами:
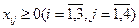
(Два учащихся выходят к доске - один записывает транспортную таблицу, другой - математическую модель задачи)
В. Опорный план транспортной задачи.
Структура опорного плана задачи:
Теорема. Ранг матрицы системы ограничительных уравнений транспортной задачи (2)-(5) на единицу меньше числа уравнений, т.е.
r=m+n-1.
(Сколько всего переменных имеет транспортная задача?) (mn)
Из теоремы следует, что каждый опорный план задачи имеет (Сколько базисных переменных?) m+n-1 базисных переменных и (Сколько свободных?) mn-(m+n-1) – свободных переменных, (Чему равны свободные переменные?) равных нулю.
Согласно сформулированной теореме, каждый опорный план будет «загружать» (Как вы думаете, что означает слово «Загружать») (Сколько клеток?) m+n-1 клеток, а остальные останутся свободными. Это не единственное требование к опорному плану. Второе связано с циклами в транспортной таблице.
Определение. Циклом в транспортной таблице называется набор клеток, в котором две и только две соседние клетки расположены в одной строке или одном столбце и последняя клетка набора лежит в той же строке или столбце, что и первая.
Графическим изображением цикла является замкнутая ломаная линия, звенья которой расположены только в строках и столбцах таблицы. Каждое звено соединяет две и только две соседние клетки цикла.
Таким образом, план транспортной задачи является опорным тогда и только тогда, когда из занятых им m+n-1 клеток нельзя образовать ни одного цикла.
При решении транспортной задачи используются следующие этапы:
1) Построение начального опорного плана;
2) Оценка этого плана;
3) Переход от имеющегося опорного плана к новому плану с меньшими транспортными затратами.
(На основании выше сказанного, учащиеся в рабочей тетради пытаются самостоятельно построить опорный план задачи, записанной в транспортной таблице)
Г. Способы построения опорного плана
Способ «северо-западного угла». Первой загружается клетка (1;1). Если закрывается строка, то следующей загружается клетка (2;1); если же закрывается столбец, то следующей загружается клетка (1;2). Итак, каждый раз загружается клетка, соседняя либо по строке, либо по столбцу (в зависимости от конкретных данных задачи). Последней будет загружена клетка (m;n). В результате загруженные клетки расположатся вдоль диагонали (1;1) – (m;n), поэтому способ «северо-западного угла» называют еще диагональным способом.
(Учащиеся читают способ «северо-западного угла» и пытаются самостоятельно построить опорный план)
 (75) (75)
|  (80) (80)
|  (60) (60)
| 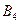 (85) (85)
| |
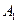 (100) (100)
|

|

| ||
 (150) (150)
|
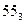
|

|
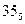
| |
 (50) (50)
|
|
(Как вы думаете, чему будет равна целевая функция?)
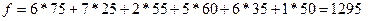 д.е.
д.е.
Способ «минимального элемента». Первой в распределительной таблице загружается клетка с наименьшим тарифом. Далее загружается клетка той же строки (столбца) со следующим по величине тарифом и т.д.
Поскольку при заполнении таблицы учитываются величины тарифов, то, как правило, построенный план оказывается ближе к оптимальному, нежели построенный способом «северо-западного угла».
(Учащиеся читают способ «минимального элемента» и пытаются самостоятельно построить опорный план)
 (75) (75)
|  (80) (80)
|  (60) (60)
| 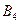 (85) (85)
| |
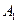 (100) (100)
|
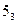
|

|
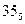
| |
 (150) (150)
|

|
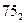
| ||
 (50) (50)
|
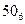
|
(Как вы думаете, чему будет равна целевая функция?)
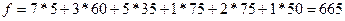 д.е.
д.е.
(Разбор ошибок?)
(Почему построенные нами планы являются опорными?) (Проверка двух условий)
Д. Оценка опорного плана
Оценка опорного плана связана со следующим свойством циклов: если в транспортной таблице содержится опорный план, то для каждой свободной клетки можно образовать один, и притом только один, цикл, содержащий эту свободную клетку и некоторую часть загруженных клеток. Эти циклы изображаются в транспортной таблице контурами, одна вершина которых находится в свободной клетке, а остальные – только в загруженных.
Пусть клетка (k;s) свободная, построим для нее цикл и обозначим алгебраическую сумму тарифов следующим образом.
 (6)
(6)
Величина 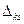 называется оценкой свободной клетки (k;s).
называется оценкой свободной клетки (k;s).
Если оценка свободной клетки отрицательная, то её следует загружать, такие клетки называются перспективными. Если же оценки всех свободных клеток неотрицательные, то содержащийся в распределительной таблице опорный план является оптимальным.
Пример 2: Исследовать построенный опорный план транспортной задачи на оптимальность. (Учащиеся по очереди выходят к проектору и находят оценку каждой свободной клетки)
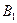 (75) (75)
| 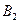 (80) (80)
|  (60) (60)
| 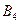 (85) (85)
| |
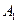 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
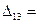 3-5+2-7=-7
3-5+2-7=-7
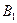 (75) (75)
| 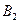 (80) (80)
|  (60) (60)
| 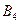 (85) (85)
| |
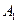 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
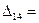 5-6+2-7=-6
5-6+2-7=-6
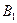 (75) (75)
| 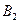 (80) (80)
|  (60) (60)
| 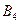 (85) (85)
| |
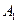 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
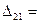 1-6+7-2=0
1-6+7-2=0
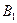 (75) (75)
| 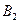 (80) (80)
|  (60) (60)
| 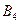 (85) (85)
| |
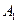 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
 3-6+7-2+6-1=7
3-6+7-2+6-1=7
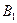 (75) (75)
| 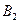 (80) (80)
|  (60) (60)
| 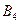 (85) (85)
| |
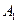 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
 10-2+6-1=13
10-2+6-1=13
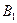 (75) (75)
| 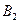 (80) (80)
|  (60) (60)
| 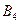 (85) (85)
| |
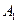 (100) (100)
| ||||
 (150) (150)
|
60 
| |||
 (50) (50)
|
 20-5+6-1=20
20-5+6-1=20
(Какие действия мы должны произвести, чтобы определить является ли опорный план, содержащийся в транспортной таблице, оптимальным?)
V. Закрепление изученного материала:
А. Решение типовой задачи
Три завода производят однородную продукцию в количестве 650, 850 и 700 единиц соответственно. Эта продукция требуется четырем потребителям в количествах 500, 800,300 и 600 единиц каждому. Затраты на перевозку единицы продукции (тыс.руб.) от каждого завода к каждому потребителю заданы матрицей: 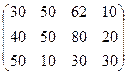 . Свести исходные данные в транспортную таблицу. Составить математическую модель задачи. Построить опорный план «северо-западным углом» и способом «минимального элемента». Исследовать построенные планы на оптимальность
. Свести исходные данные в транспортную таблицу. Составить математическую модель задачи. Построить опорный план «северо-западным углом» и способом «минимального элемента». Исследовать построенные планы на оптимальность
Б. Самостоятельная работа (приложение А)
В. Коллективное решение текстовых задач повышенной сложности (приложение Б)
Поиск по сайту: