Примечания ряда Тейлора для численного дифференцирования

На практике формулы численного дифференцирования находят с использованием ряда Тейлора. Разлагая функцию f(x) в ряд Тей­лора по степеням h,где h достаточно мало, имеем:

(2.46а)

(2.46б)

По формулам (2.46а) и (2.46б)

экв. (2.47а)

экв. (2.47б)

Вычитая соотношение (2.46б) из (2.46а), получаем:

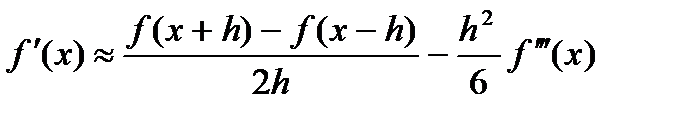(2.48)

Очевидно, что формулы для первой производной (2.43а) и (2.47а), (2.436) и (2.476), (2.446) и (2.48) представляют собой по­парно эквивалентные записи. При сравнении этих формул нужно полагать x=x₀ в (2.47а) и x=x₁в (2.476) и (2.48).

Складывая соотношения (2.46а) и (2.466), получаем для второй производной:

(2.49)

Очевидно, что формулы (2.456) и (2.49) эквивалентны, если в (2.49) полагать x=x₁.

Поиск по сайту: