АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка задачи численного интегрирования

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  3. I. Ситуационные задачи и тестовые задания.
  4. II. Основные задачи и функции
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  8. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  9. Аналитические возможности, задачи и основные направления анализа СНС
  10. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА
  11. БЖД: цель, задачи, роль в подготовке специалиста, основные категории
  12. Билет 1. Предмет истории как науки: цели и задачи ее изучения

В тех случаях, когда при вычислении определенного интеграла

(2.50)

Первообразная функция F(x) не может быть найдена с помощью элементарных средств или является слиш­ком сложной; вследствие этого вычисление определенного интеграла по формуле (1) может быть затруднительным или даже практически невыполнимым.

Кроме того, на практике подынтегральная функция f(x) часто задается таблично и тогда само понятие первообразной теряет смысл. Аналогичные вопросы возникают при вычислении кратных интегра­лов. Поэтому важное значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.

Задача численного интегрирования функции заключается в вычи­слении значения определенного интеграла на основании ряда значе­ний подынтегральной функции.

При этом подынтегральную функцию f(x) заменяют такой приближающей, что она, во-первых, близка в каком-то смысле к f(x):

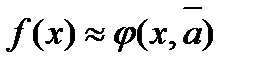
а, во-вторых, интеграл от легко вычисляется. Чаще всего подынтегральную функцию заменяют интерполяционным много­членом Лагранжа:

(2.51)

в котором Rn(x) — остаточный член интерполяции. Подставляя этот многочлен (2.51) в (2.50), получаем:

Где - остаточный член формулы численного ин­тегрирования или ее погрешность.

Заменяя f(x) интерполяционными многочленами различной степени, получают формулы численного интегрирования различ­ного порядка точности.

 


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)