Постановка вопроса

Приближенное дифференцирование.

При решении практических задач часто нужно найти производ­ные указанных порядков от функции y— y=f(x),заданной таблично. Возможно также, что в силу сложности аналитического выражения функции f(x)непосредственное дифференцирование ее затрудни­тельно. В этих случаях обычно прибегают кприближенному, дифференцированию.

Для вывода формул при­ближенного дифференцирова­ния заменяют данную функцию f(x) на интересующем от­резке [a,b] интерполирующей функцией P(x) (чаще всего по­линомом), а затем полагают:

(1)

при

Аналогично поступают при нахождении производных высших порядков функции f(x).

Если для интерполирующей функции P(x) известна погрешность.

то погрешность производной выражается формулой:

(2)

т. е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же самое справедливо и для производных высших порядков.

Следует отметить, что, вообще говоря, приближенное дифферен­цирование представляет собой операцию менее точную, чем интер­полирование. Действительно, близость друг к другу ординат двух кривых:

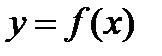и

на отрезке [a, b] еще не гарантирует близости на этом отрезке их производных и 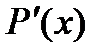,т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одина­ковых значениях аргумента (рис. 65).

Таким образом, точность расчета производной при заданной степени интерполяционного многочлена уменьшается с увеличе­нием номера производной. При решении практических задач, в том числе при численном решении обыкновенных дифференци­альных уравнений и уравнений в частных производных, прихо­дится использовать аппроксимации первых и вторых производ­ных. Значительно реже приходится аппроксимировать производ­ные более высоких порядков.

Поиск по сайту: