АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Физический смысл производной

Читайте также:
  1. А. Физический и умственный труд.
  2. Абсолютно упругий и неупругий удар тел. Внутренняя энергия. Общефизический закон сохранения энергии
  3. Алекс с таким удовольствием начал рассказывать, поясняя смысл текстов, что совсем забылся.
  4. Бессмысленное истощение земель
  5. Билет 45. Философский смысл сознания. Проблема сознания в истории философии.
  6. Билет № 17 Философский смысл эпохи просвещения
  7. Биологический смысл основных религиозных понятий. Краткий словарь
  8. Биологический смысл основных религиозных понятий. Краткий словарь.
  9. Будущее бессмысленно
  10. Бытовой уровень. Что такое счастье и смысл жизни
  11. Бытовой уровень. Что такое счастье и смысл жизни.
  12. В материальном смысле В формальном смысле

Основы дифференциального исчисления. Понятие производной.

DX=X1-X – приращение аргумента.

Df(X)=f(X+DX)-f(X) – приращение функции. Пример:

Определение: Произв. функ. f(x) в точке Х наз. предел отношения приращения функ. к приращению аргум., когда последнее стремится к 0.

Геометрический смысл производной.

Ку.к. – угловой коэф. касательной.

Ксек – угловой коэф. секущей.

Таким образом угловой коэффициент касательной совпадает со значение производной в данной точке.

Уравнение касательной к графику функции y=f(x) в точке М0 (x0,y0) имеет вид:

Физический смысл производной.

S(t) – путь за данное время.

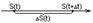
DS(t) – приращение пути.

DS(t)/ Dt –средняя скорость на участке.

мгновен. скорость на участке: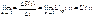

произв. пути от скорости: S'(t)=U(t)

Теорема: Связь между непрерывной и дифференцируемой функцией.

Функция наз. диферинцируемой если она имеет производную.

Если функция диффер. в точке х, то она и непрерывна в этой точке.

Доказательство:

 


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)