Аналитическая геометрия

12. Виды уравнений прямой на плоскости. Расстояние от точки до прямой.

Виды:

1) Общее уравнение прямой: Ax + By + C = 0

2) Уравнение прямой в отрезках: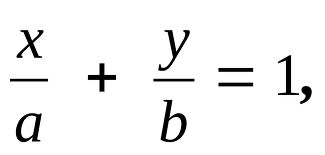

3) Уравнение прямой с угловым коэффициентом: y = kx + b

4) Каноническое уравнение прямой на плоскости: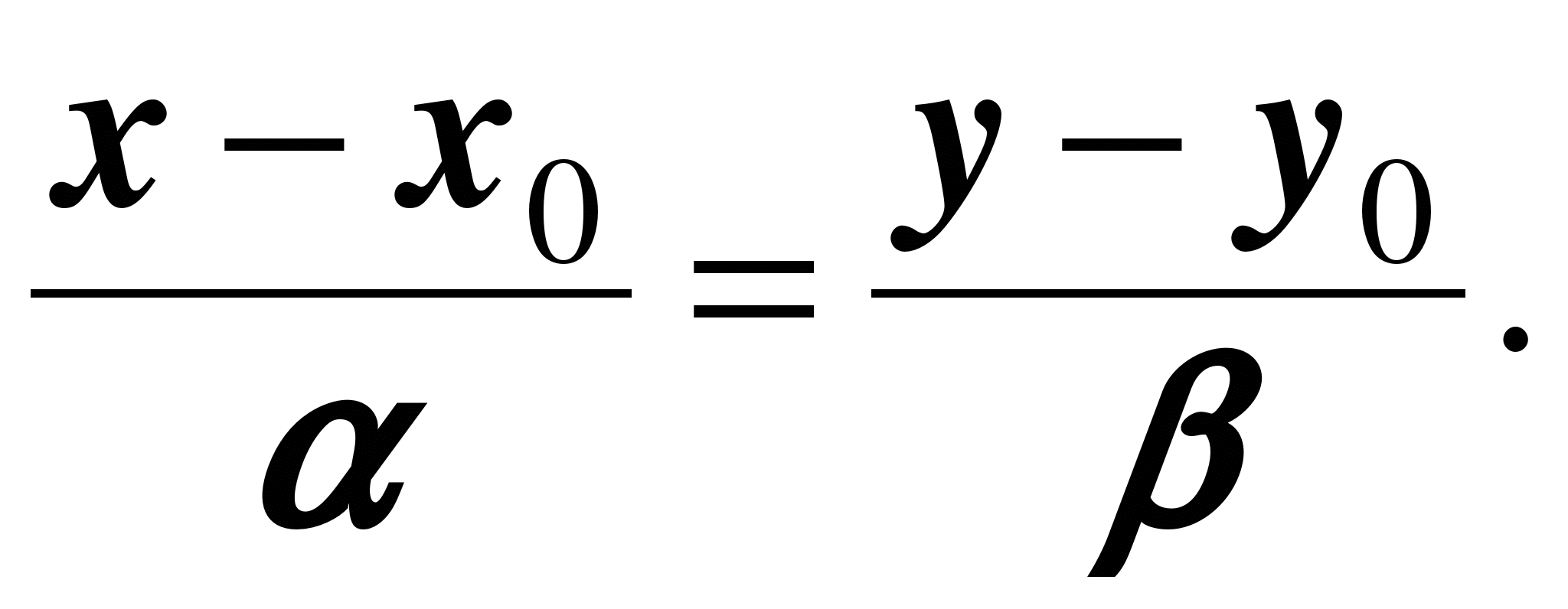

5) Параметрические уравнения прямой на плоскости: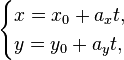

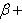
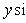
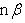
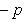
6) Нормальное уравнение прямой: 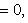p - длина перпендикуляра, опущенного из начала координат на прямую, β - угол наклона этого перпендикуляра к оси O.

Расстояние точки A (x ₁, y ₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле:

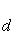
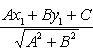
13. Взаимное расположение двух прямых на плоскости, угол между прямыми.

Если прямые 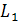и 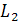заданы общими уравнениям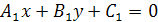и и ,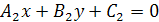

тогда угол между ними находится по формуле: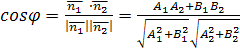

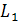– условие параллельности прямых и ;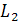

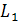– условие перпендикулярности прямых и .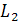

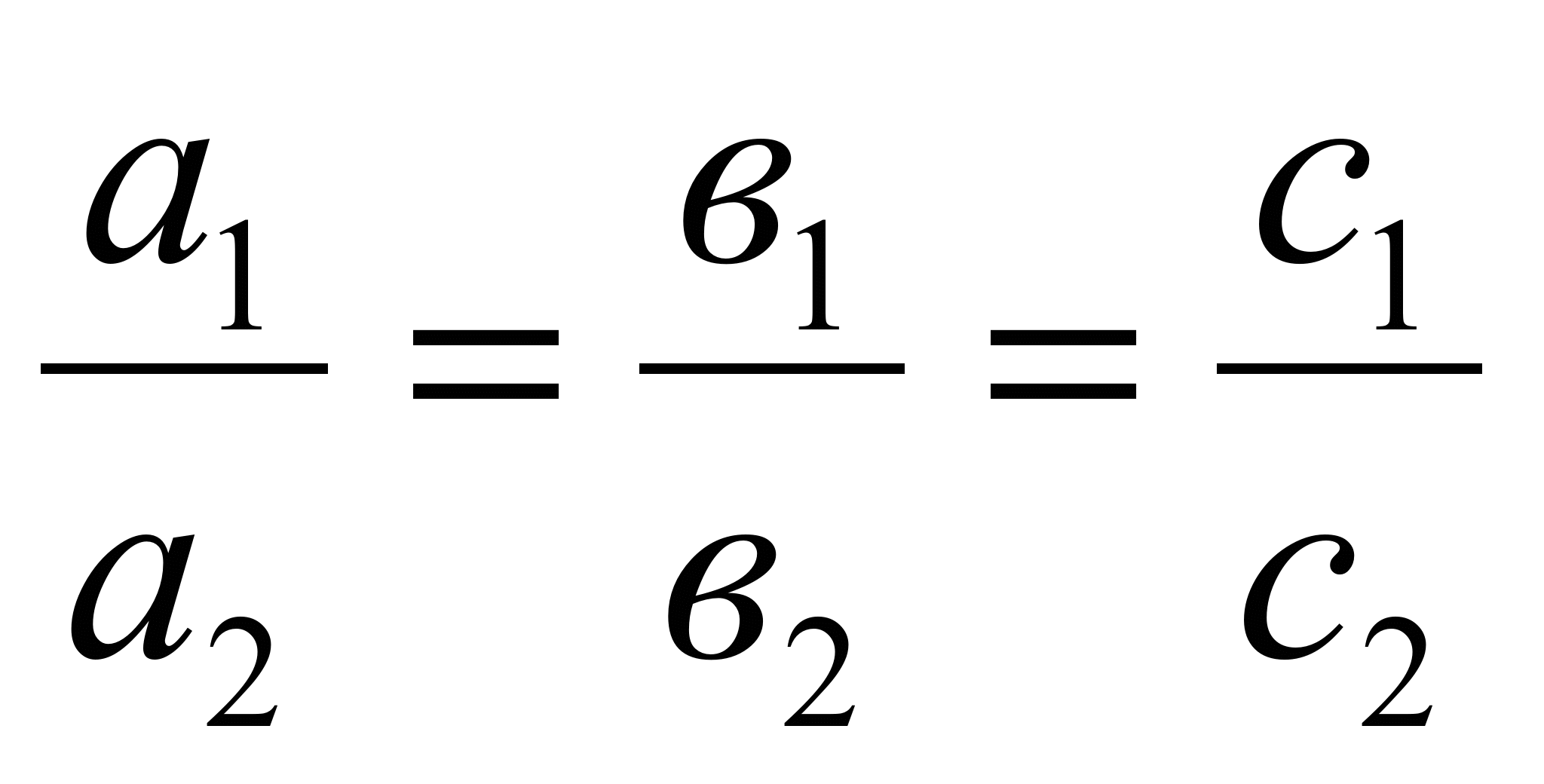- прямые совпадают.

14. Виды уравнений плоскости. Расстояние от точки до плоскости.

Виды уравнений плоскости:

1) Общее: Ax + By + Cz + D = 0

2) В отрезках:

3) Нормальное: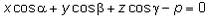

Пусть плоскость 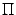задана уравнением Ax + By + Cz + D = 0 и дана точка 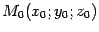. Тогда расстояние p от точки _Mo до плоскости 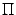определяется по формуле

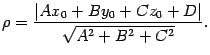
15. Взаимное расположение двух плоскостей, угол между плоскостями.

Взаимное расположение двух плоскостей характеризуется двумя возможностями^

1) Две плоскости не имеют общих точек, и, в таком случае, они называются параллельными

2) Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися.

Пусть наши плоскост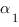и и 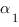заданы уравнениями:

: :

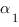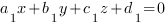
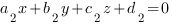
Косинус угла 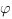между плоскостями находится по такой формуле:

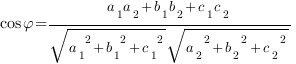
1) Плоскости параллельны: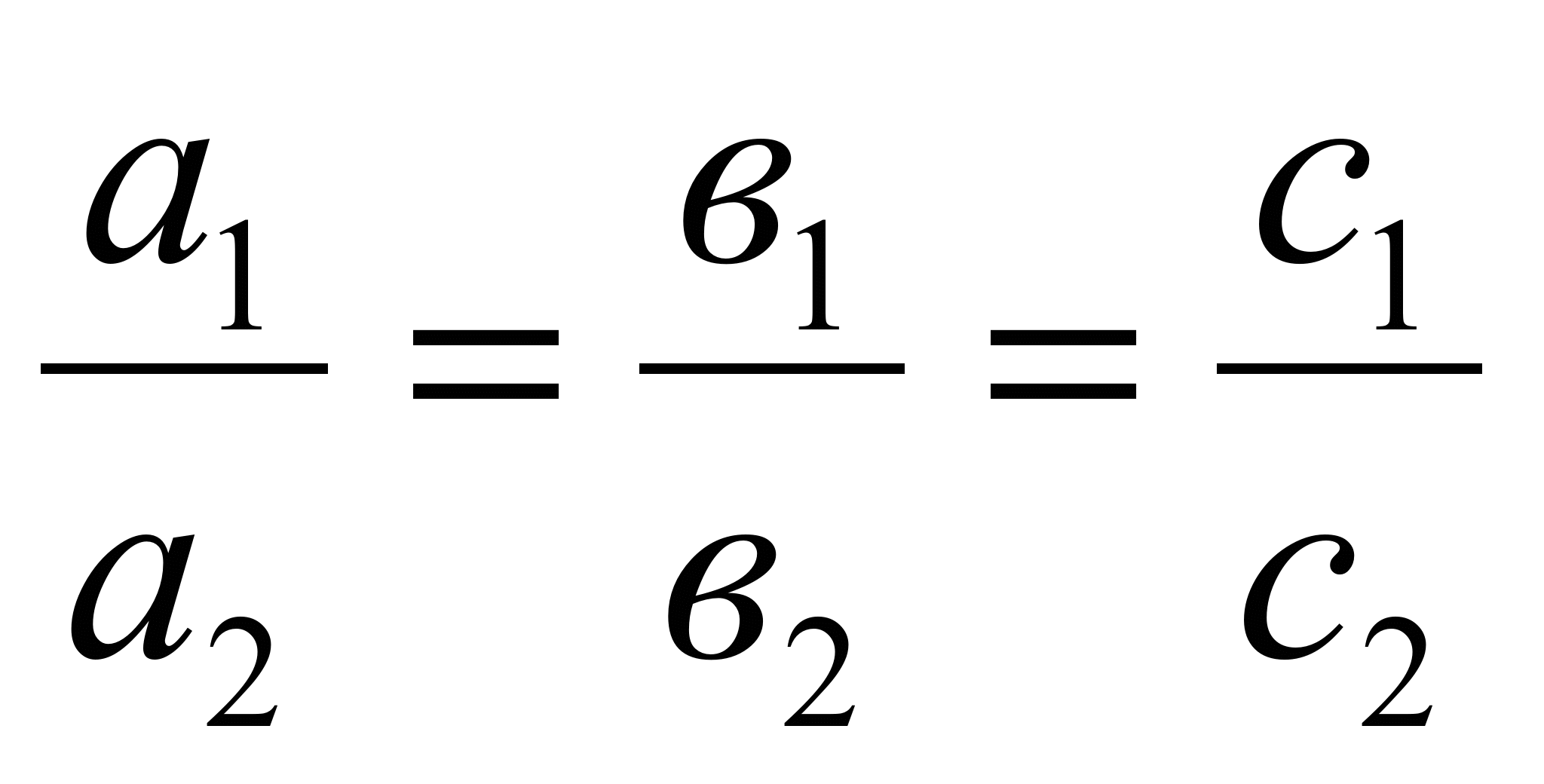

2) Плоскости совпадают, если выполняются следующие условия:

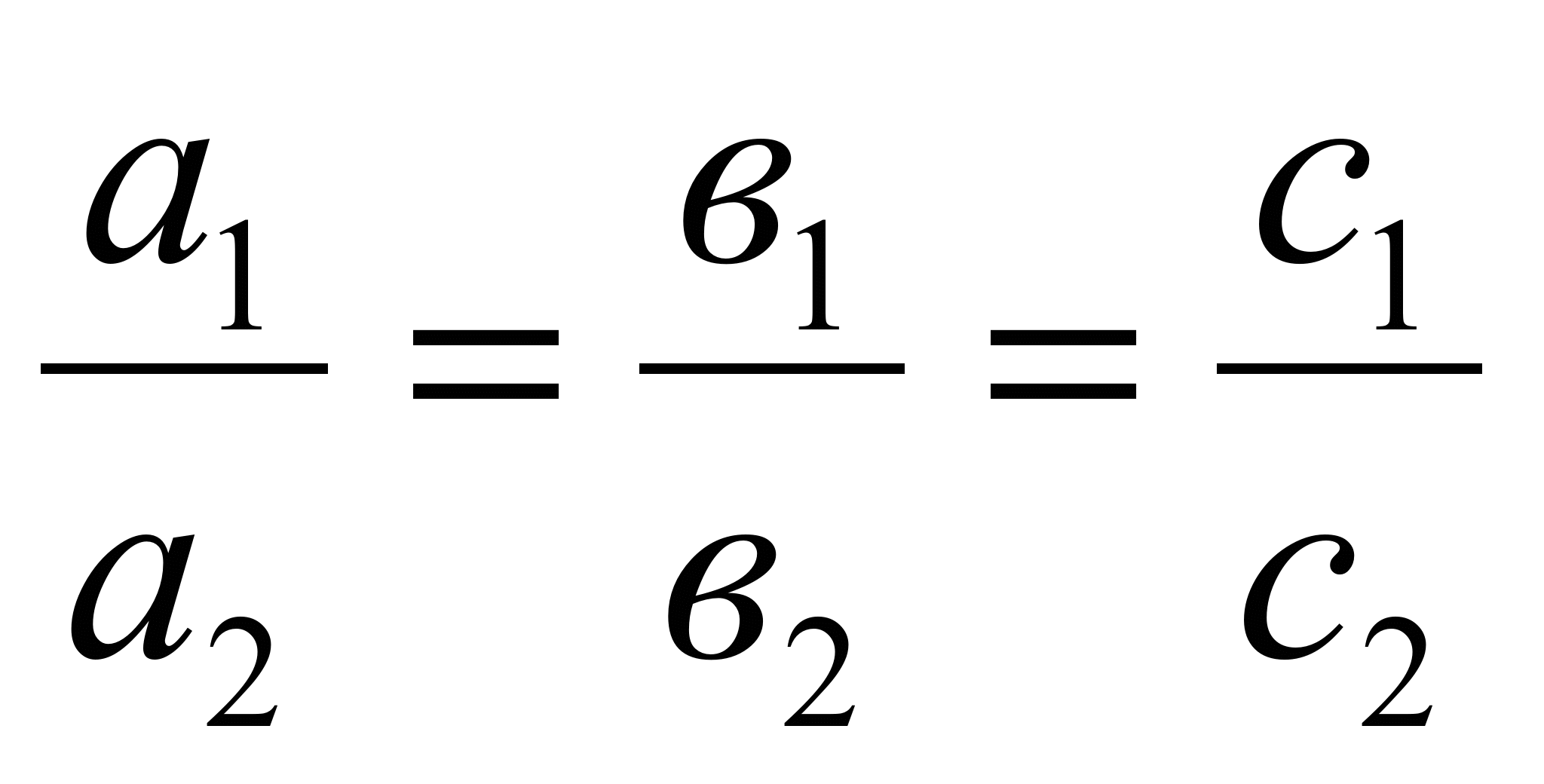
a₂*x₀ + b₂*y₀ + c₂*z₀ + d₂ = 0

существует точка M₀(x₀,y₀,z₀), принадлежащая плоскости П₁

16. Виды уравнений прямой в пространстве. Расстояние от точки до прямой.

Виды:

1) Прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей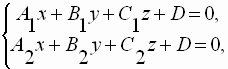

2) Параметрические уравнения прямой в пространстве: 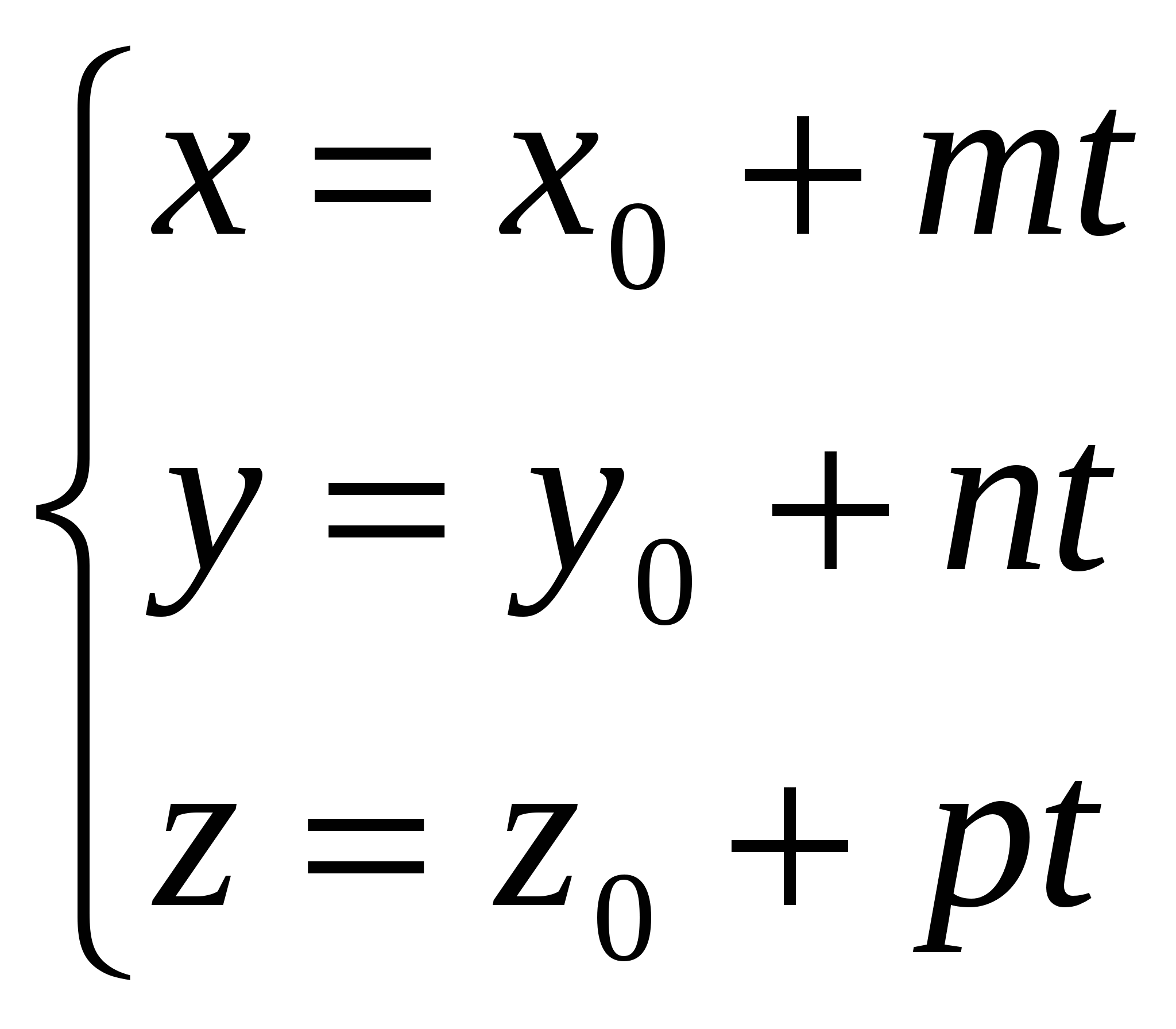где x₀, y₀ и z₀ – координаты некоторой точки прямой, m, n, p - соответствующие координаты направляющего вектора прямой, а t - некоторый параметр.

3) Каноническое уравнение прямой в пространстве: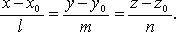

Расстояние от точки до прямой: 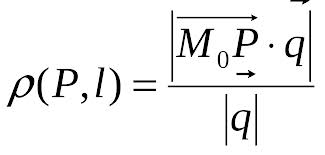, | | 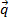- длина вектора прямой, M_o – точка, лежащая на прямой l, P – точка.

17. Взаимное расположение двух прямых в пространстве, угол между прямыми.

1) Прямые скрещиваются: (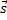, , 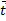) ≠ 0

2) Прямые параллельны: (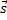, , 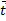) = 0, ||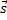

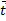
3) Прямые пересекаются (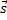, , 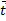) = 0, 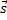не параллельна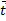

Угол между прямыми a и b: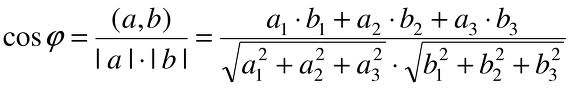

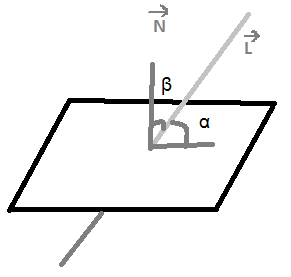
18. Взаимное расположение прямой и плоскости, угол между ними.

Плоскость: A_x + B_y + C_z + D = 0

Прямая: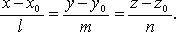

1) Параллельны: A_l + B_m + C_n = 0

2) Перпендикулярны: = =

3) Прямая лежит в плоскости: A_l + B_m + C_n = 0 и Ax_o + By_o + Cz_o + D = 0

Угол между плоскостью и прямой:

Sin α = cos β = cos ( ) = =

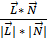19. Каноническое уравнение эллипса, эксцентриситет, директриса.

Эллипс - геометрическое место точек, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная, бОльшая, чем расстояние между данными точками.

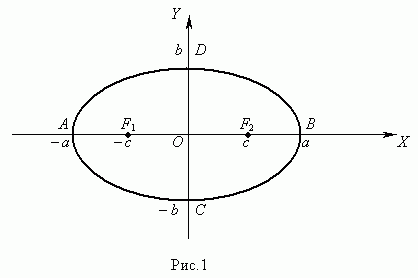
Эксцентриситет - отношение фокусного расстояния к большей оси: E =

Директрисы эллипса - две прямые, которые в канонической для эллипса системе координат имеют уравнения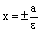

20. Канонические уравнение гиперболы, эксцентриситет, директриса, асимптоты.

Гипербола - геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек (фокусов) есть величина постоянная, мЕньшая, чем расстояния между этими точками.

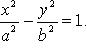
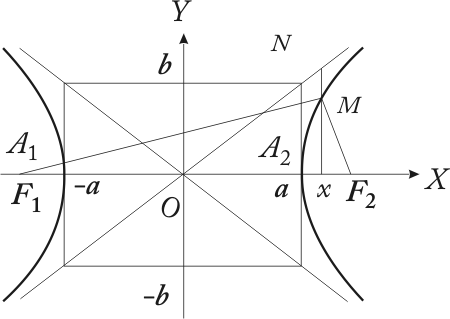
Эксцентриситет - отношение фокусного расстояния к большей оси: E =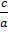

Директрисами гиперболы называются две прямые, уравнения которых в канонической для гиперболы системе координат имеют вид.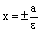

Прямая называется асимптотой кривой, если при удалении от начала координат расстояние между кривой и асимптотой стремится к нулю.

Прямые 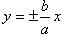называются асимптотами гиперболы.

21. Каноническое уравнение параболы

Парабола – геометрическое место точек, равноудалённых от заданной точки, называемой фокусом и от заданной прямой, называемой директрисой.

P – расстояние между фокусом и директрисой параболы.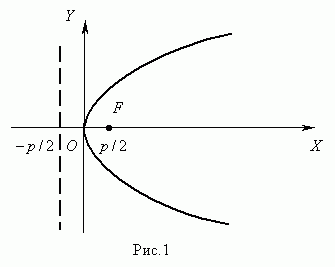

22. Поверхности 2-го порядка. Эллипсоид. Гиперболоид. Конус.

Общий вид поверхности 2-го порядка: Ax² + By² + Cz² + Dxy + Eyy + Fzx + Lx + My + Nz + K = 0

1) Эллипсоид

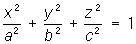
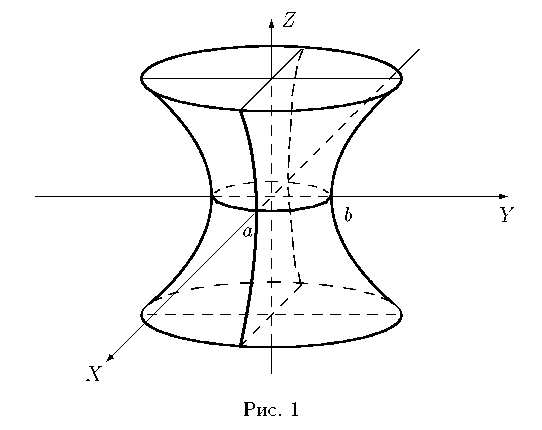
2) Однополостный гиперболоид (рис. 1) -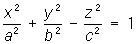

Двуполостный гиперболоид (рис. 2) -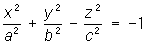

3) Конус

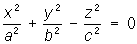
23. Эллиптический и гиперболический параболоиды.

Эллиптический параболоид: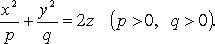

Гиперболический параболоид: 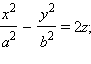a > 0, b >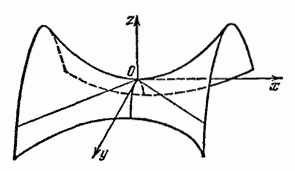

24. Поверхности вращения.

Пусть L – прямая в плоскости P. Будем вращать P вокруг прямой L, тогда точки некоторой кривой в плоскости P будут описывать поверхность, состоящую из окружности. Такая поверхность называется поверхностью вращения.

Каноническое уравнение эллипсоида: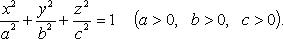

При a = b Получится эллипсоид вращения вокруг оси Oz

При a = c – вокруг оси Oy (рис. 29)

При b = c – вокруг оси Ox

При a = b = c - сфера

25. Цилиндрические поверхности.

Любое уравнение f (x,y) = 0 можно рассматривать как цилиндрическую поверхность с образующей параллельной OZ и направляющей кривой F (x,y) = 0.

Если уравнение F (x,y) = 0 определяет кривую 2-го порядка, то она называется цилиндрической поверхностью 2-го порядка.

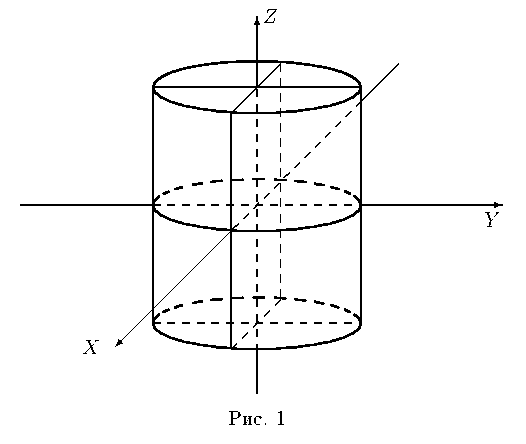
1) Эллиптический цилиндр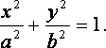

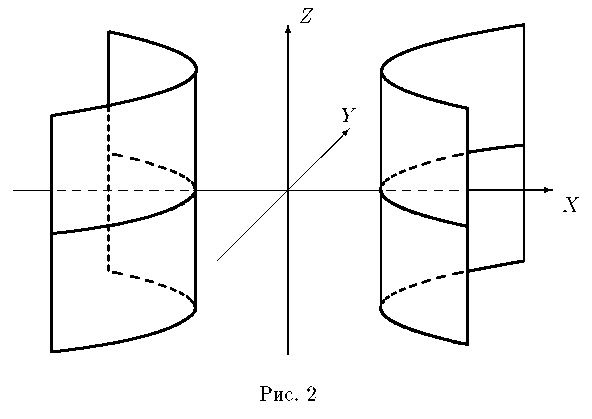
2) Гиперболоид цилиндрический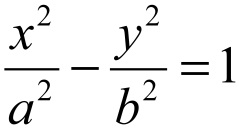

3) Параболический цилиндр: y² = 2px (p>0)

Поиск по сайту: