Векторная алгебра. 7. Линейные операции над векторами

7. Линейные операции над векторами. Базис.

Вектор – направленный отрезок прямой, у которого один конец – начало, а другой – конец.

Линейные операции над векторами:

1) Умножение вектора на число.

, α ϵ R => = α *

1) | | = |α|*| |

2) ||

3) α > 0 => ↑↑

α < 0 => ↑↓

α = 0 => =

2) Сложение векторов. Складываются по правилу треугольника или параллелограмма.

свойства:

1) + = +

2) ( + ) + = + ( + )

3) + =

4) - = (-1)*

5) α ( + ) = α* + α* , α ϵ R

6) (α + β) = α* + *β

3) Разность векторов.

- = + (-1)* = *β

Базис – упорядоченный набор компланарных векторов в пространстве.

Представление вектора в виде линейной комбинации векторов называется разложением вектора по базису, а коэффициент этого разложения – координатами вектора в этом базисе.

- базисы трёхмерного пространства.

8. Проекция вектора на ось. Прямоугольная система координат. Координаты точки. Линейные операции над векторами в координатной форме.

Свойства проекций:

1) Проеция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:

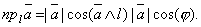
2) Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:

3) Если вектор умножается на число λ, то его проекция на ось также умножается на это число

ПСК – система координат с базисом , , , 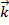удовлетворяющий условиям:

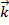1) | | = | | = | | = 1

2) , , 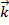перпендикулярны друг другу.

Координаты точки: Пусть a, b, c – единичные векторы осей координат, O – начало координат. Тогда координаты произвольной точки P – это координаты вектора относительно базиса (a, b, c).

Линейные операции над векторами в координатной форме:

1. Равные векторы имеют равные координаты (в одном и том же базисе).

2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.

3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.

4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.

9. Скалярное произведение векторов, его свойства. Вычисление в координатах.

Скалярным произведением векторов и называется произведение их длин на косинус угла между ними:

Свойства:

1) * = *

2) (α * ) = (α* )* = α*( *

3) ( + ) * = * + *

4) * = | |²

5) , ≠

* > 0 0 < угол (; ) <

* < 0 < угол (; ) < π

* = 0 перпендикулярен

10. Определение правой тройки векторов. Векторное произведение векторов, его свойства, геометрический смысл.

Тройка векторов , и называется правой, если направлен так, что из его конца кратчайший поворот от к происходит против часовой стрелки.

Векторным произведением вектора на вектор называется третий вектор который обладает следующими свойствами:

1. Его длина равна

2. Вектор перпендикулярен к плоскости, в которой лежат вектора и

3. Вектор направлен так, что поворот от вектора к вектору осуществляется против часовой стрелки, если смотреть из конца вектора (тройка векторов , и – правая).

Основные свойства векторного произведения:

1) Векторное произведение равно нулю, если векторы и коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный

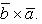
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.

11. Смешанное произведение 3-х векторов, его свойства. Геометрический смысл. Вычисление в координатах. Необходимое и достаточное условие компланарности 3-х векторов.

Смешанным произведением векторов , , называется число, равное ( * )* = (, , )

Модуль смешанного произведения векторов , , равен объёму параллелепипеда, построенного на векторах , , .

Свойства:

1) ( * )* = *( * )

2) (, , ) = (, , ) = (, ) = - (, , ) =... циклически меняем

3) , , – компланарны (, , ) = 0

4) , , – правая (, , ) > 0

, , – левая (, , ) < 0

5) ( ₁ + ₂, , ) = ( ₁, , ) + ( ₂, , ) (α* , , ) = α (, , )

Вычисление в координатах: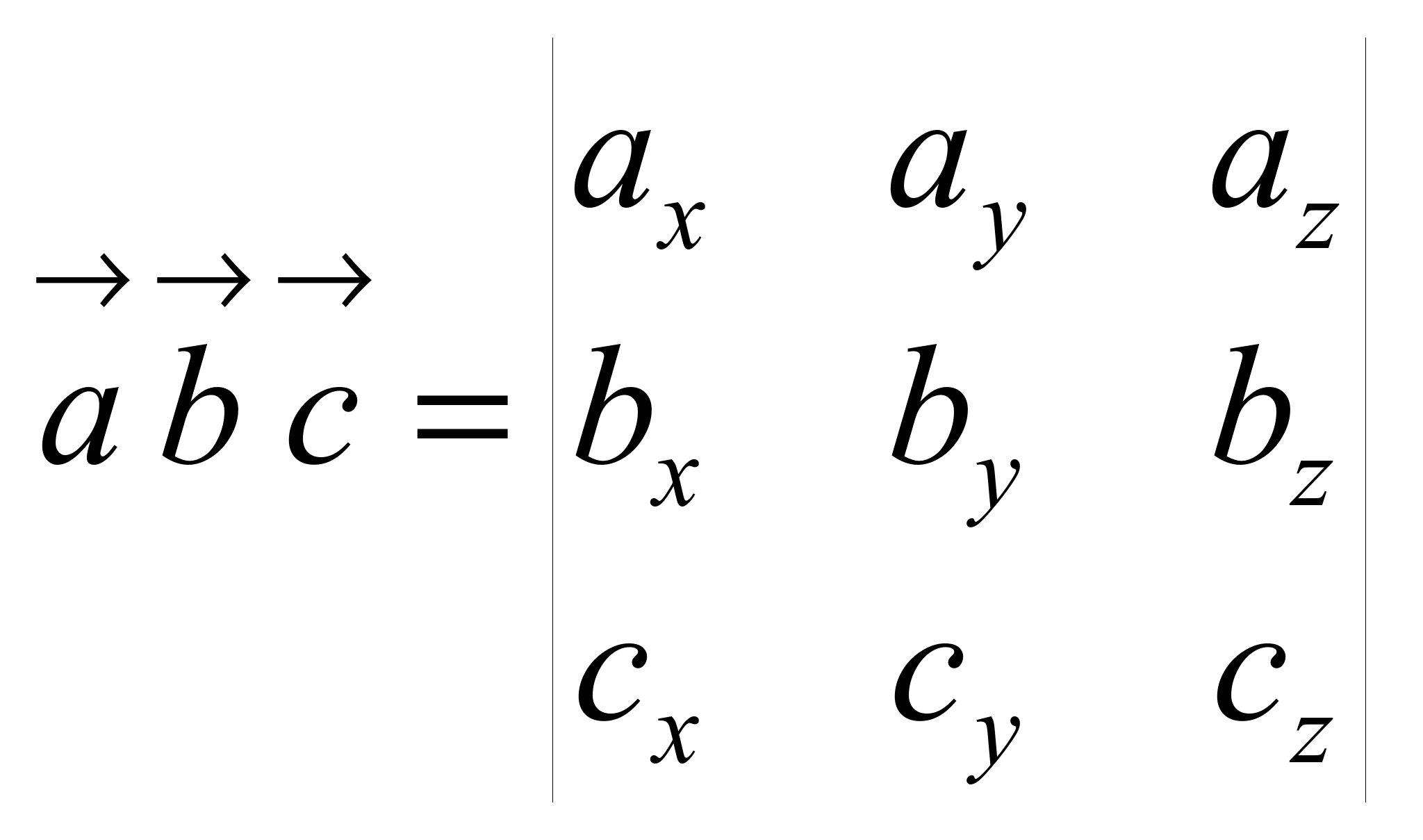

Необходимое и достаточное условие компланарности 3-х векторов:

Поиск по сайту: