 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Дифференциальное исчисление функции одной переменной
26. Понятие функции. Способы задания функции. Свойства функций. Обратная функция.
Пусть x, y ≠ 0. Функция – соответствие f, по которому любой x, принадлежащий множеству X сопоставлено единственному y, принадлежащему множеству Y. y = f(x)
Способы задания функции:
1) Аналитический
2) Табличный
3) Графический
4) Словесный
Свойства функции:
1) чётность/нечётность чётная (симметрична относительно Oy), если f(-x) = f(x);
нечётная (симметрична относительно начала координат), если f(-x) = -f(x)
2) Возрастание\убывание
3) Ограниченность. f(x) ограничена, если существует M > 0, такое, что f(x) < M (или f(x) > M, если ограничена снизу) при любом x.
4) Периодичность. Функция f(x) называется периодической с периодом T > 0, если f(x) = f (x + T), при любом x.
Пусть X – область определения, а Y – область значений функции f. Если для любого y из области значений существует единственный x, принадлежащий области определения, то говорят, что определена обратная функция к y = f(x) (f-1)
Любая монотонная функция обладает обратной функцией.
Геометрический смысл: Функция и обратная к ней функция симметрична относительно y = x.
27. Основные элементарные функции и их графики.
1)
1) y = xn, n > 1 
2) y = 

3) y =  , n > 1
, n > 1
2) y = ax 
1) a >1
2) 0 < a < 1
3) y = log a x 
1) a > 1
2) 0 < a < 1
4) y = sin x, cos x, tg x, ctg x



5) y = arcsin x, arccos x, arctg x, arcctg x


6) y = ex
28. Предел числовой последовательности. Бесконечно большие и бесконечно малые числовые последовательности. Свойства бесконечно малых.
Число а называется пределом числовой последовательности xn, если любой E-определенности > 0 существует N, меньшее любой n => |xn-a|< E-определённости, т.е. xn принадлежит E -определенности.
Последовательность {αn} называется бесконечно малой, если  = 0
= 0
Последовательность {xn} называется бесконечно большой, если {  } – бесконечно малая
} – бесконечно малая
Свойства бесконечно малых:
1) αn +  n – бесконечно малая
n – бесконечно малая
2) αn *  n – бесконечно малая
n – бесконечно малая
3) αn * с – бесконечно малая, c – действительное число
4) αn *  n – бесконечно малая, xn – ограниченная
n – бесконечно малая, xn – ограниченная
29. Основные теоремы о пределах последовательностей.
1) Если предел последовательности существует, то он единственный
2) Сходящаяся последовательность ограничена.
Следствие: Если последовательность не ограничена, то она расходящаяся.
3) A =  <=> xn = A + αn, где αn - бесконечно малая.
<=> xn = A + αn, где αn - бесконечно малая.
4) Теорема о милиционерах: Пусть существует  = a. Существует
= a. Существует  = a
= a
αn <= xn <=  n, любое n.
n, любое n.
Тогда  = a
= a
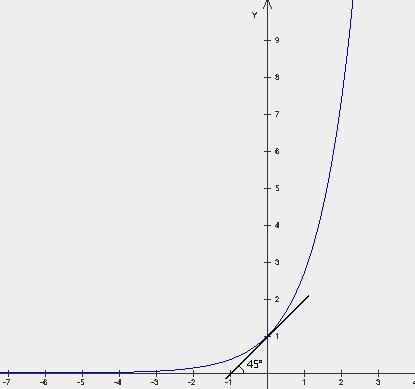
30. Первый и второй замечательные пределы. Число е.
Первый замечательный предел: αn – бесконечно малая, то  = 1
= 1
Второй замечательный предел:  )n = e
)n = e
Число «e» (2,718...) —иррациональное. Вычисляется с помощью следующего ряда: 
Число e есть предел выражения 
31. Предел функции. Основные теоремы о пределах функций.
Число A называется пределом функции f(x) в точке x = a (или при x -> a), если всякая окрестность > 0
A = 
Теоремы:
1) Предел постоянной равен самой постоянной
2) Постоянный множитель можно выносить за знак предела:  = k *
= k * 
3) Предел суммы (разности) функций равен сумме (разности) пределов этих функций:  =
=  ±
± 
4) Предел произведения функций равен произведению пределов этих функций:
 =
=  *
* 
5) Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:  =
=  ,
,  ≠ 0
≠ 0
32. Замечательные пределы для функций.
1)  = 1
= 1
Доказательство: Из доказательства замечательного предела для последовательности имеем 1 
 ≤ cos αn
≤ cos αn
1 ≥  ≥ cos x
≥ cos x
По теореме о милиционерах в силу  = 1 получаем
= 1 получаем  = 1
= 1
2)  = e
= e
Доказательство: n = [x] – целая часть x. Рассмотрим случай x --> +∞, x > 0
n ≤ x < n + 1 =>  <
<  ≤
≤  => 1 +
=> 1 +  < 1 +
< 1 +  ≤ 1 +
≤ 1 + 
Возводим в степень n ≤ x < n + 1
 < (1 +
< (1 +  ≤
≤ 
 =
=  =
= 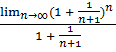
 =
=  =
=  (1 +
(1 +  ) = e * 1 = e
) = e * 1 = e
по теореме о милиционерах:
 = e
= e
Рассмотрим случай x --> -∞
 = [t = -x] =
= [t = -x] =  =
=  =
= 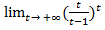 =
= 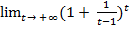 =
=  *
*  = e*1 = e
= e*1 = e
33. Сравнение бесконечно малых. Эквивалентные бесконечно малые.
Сравнение бесконечно малых:
1. Если  = А (А – действительное число ¹ 0), то α и ß называются бесконечно малыми одного порядка.
= А (А – действительное число ¹ 0), то α и ß называются бесконечно малыми одного порядка.
2. Если  = 0, то α называется бесконечно малой более высокого порядка, чем ß.
= 0, то α называется бесконечно малой более высокого порядка, чем ß.
3. Если  = ∞, то α называется бесконечно малой более низкого порядка, чем ß.
= ∞, то α называется бесконечно малой более низкого порядка, чем ß.
4. Если  не существует, то α и ß называются несравнимыми бесконечно малыми.
не существует, то α и ß называются несравнимыми бесконечно малыми.
Функция f(x) называется бесконечно малой при x --> a, если  = 0.
= 0.
Если  = 1, то α и ß называются эквивалентными бесконечно малыми (α ~ ß)
= 1, то α и ß называются эквивалентными бесконечно малыми (α ~ ß)
Теорема: Сумма бесконечно малых эквивалентна бесконечно малой более низкого порядка из этой суммы.
Таблица эквивалентных бесконечно малых:
1. sin x ~ х
2. tg x ~ х
3. arcsin х ~ х
4. arctg x ~ х
5. 1 - cos x ~ x2/2
6. ех – 1 ~ х
7. αх – 1 ~ х*ln(a)
8. ln(1+х) ~ х
9. loga(l+х) ~ х•logaе
10. (1+х)k – 1 ~ k*х, k > 0
34. Непрерывные функции. Классификация точек разрыва.
Функция f(x) называется непрерывной в точке xo, если:
1) f(x) определена в окрестность xo
2) существует  = f(x0)
= f(x0)
Замечание 1: условие 2 эквивалентно  = f(
= f(  )
)
Замечание 2: обозначим через ∆f (xo) = f (xo + ∆x) – f(xo) приращение функции f(x) при приращении аргумента ∆x = x - xo
Тогда определение 1 перепишется в виде:  = 0
= 0
Точка x0, в которой нарушается непрерывность, называется точкой разрыва.
Точка разрыва x0 называется точкой разрыва 1-го рода функции f(x), если выполнено хотя-бы одно из условий:
1) Существует  = A + < ∞
= A + < ∞
Существует  = A - < ∞
= A - < ∞
A + = A - => точка устранимого разрыва
2) A + ≠ A - => x0 точка конечного разрыва
Если хотя-бы один из пределов  или
или  не существует, или бесконечен, то точка x0 называется точкой разрыва 2-го порядка.
не существует, или бесконечен, то точка x0 называется точкой разрыва 2-го порядка.
35. Свойства непрерывных функций. Основные теоремы о непрерывных функциях.
Свойства функций, непрерывных в точке:
1) Сумма, разность и произведение двух функций, непрерывных в точке x = a, непрерывны в этой точке.
2) Если функция f(x) непрерывна при некотором значении x, то приращение функции бесконечно мало при бесконечно малом приращении аргумента.
Свойства функции, непрерывных на замкнутом промежутке:
1) Среди значений, которые принимает функция f(x) в точках незамкнутого промежутка (a,b), может не быть наибольшего или наименьшего.
2) Если m есть значение функции f(x) при x = a и n – значение f(x) при x=b, то функция f(x) принимает внутри промежутка (a,b) по крайней мере по одному разу всякое значение p, заключенное между m и n.
3) Если переменные x и x` изменяются так, что разность x – x` бесконечно малая, то разность f(x) – f (x`) тоже бесконечно малая.
Теоремы:
1) Если f(x), g(x) – непрерывны в x0, то c*f(x), где c – действительное число, f(x) + g(x), f(x)*g(x), 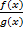 (g(x0) ≠ 0), - непрерывные функции в x0
(g(x0) ≠ 0), - непрерывные функции в x0
Если y = f(u) – непрерывна в u0, u =  (x) – непрерывна в x0,
(x) – непрерывна в x0,  (x0) = uo, то композиция функции y = f(
(x0) = uo, то композиция функции y = f( (x)) непрерывна в xо
(x)) непрерывна в xо
2) Все элементарные функции непрерывны в своей области определения
3) Функция, непрерывная на отрезке достигает своего минимума и максимума значений
4) Функция, непрерывная на отрезке принимает все промежуточные значения
f(a) = A, f(b) = B, A<B, f(x) – непрерывна на [a,b] =>любое c принадлежит [A,B] => существует x0 принадлежит [a,b] f(x0) = c
36. Определение производной, ее геометрический смысл.
Пусть функция y = f (x) определена в некоторой окрестности точки xо и существует конечный предел отношения. Тогда этот предел называется производной функции в точке xо

Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции y = f(x) в точке xo равен производной функции
y = f(x) в этой точке: 
37. Дифференцируемость и непрерывность. Правила дифференцирования.
Функция y=f(x) называется дифференцируемой в точке xo , если ее приращение Δy в точке xo может быть представлено в виде: Δy = A*Δx + α(Δx) * Δx, где A - некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е.  = 0.
= 0.
Теорема
Для того, чтобы функция y=f(x) была дифференцируема в точке xo, необходимо и достаточно, чтобы она в этой точке имела конечную производную.
Говорят, что функция f (x) является непрерывной в точке a (a – действительное число), если для любой последовательности {xn}, такой, что

выполняется соотношение

Правила дифференцирования:
1) (c*f(x))` = c * f `(x)
2) (f(x) ± g(x))` = f `(x) ± g` (x)
3) (f(x) * g(x))` = f `(x) * g (x) + f (x) * g`(x)
4)  )` =
)` = 
38. Производная сложной функции, функции, заданной неявно, заданной параметрически, обратной функции.
Пусть y=f(u) – дифференцируема в uo, u=g(x)- дифференцируема в xo, uo = g(xo), тогда сложная функция y = f(g(x)) дифференцируема в xo и y`= f `(g(x)*g`(x))
Функция задана неявно, если она задана уравнением f(x,y) = 0 не разрешённым относительно y.
Для нахождения производной y`x от неявно заданной функцией F(x,y) = 0 достаточно продифференцировать это уравнение по x, рассматривать y, как функцию от x и полученное уравнение решить относительно y`.
Пусть x(t), y(t) – дифференц, ф x(t) имеет обратную функцию t = t(x). Тогда y` = y(t(x))
y`x = y`t * t`x = 
Пусть функция  имеет в точке
имеет в точке  производную
производную  . Тогда обратная функция
. Тогда обратная функция  имеет в соответствующей точке
имеет в соответствующей точке 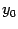 производную
производную  , которую можно отыскать по формуле
, которую можно отыскать по формуле

|
39. Производные основных элементарных функций.

40. Дифференциал. Формула df(x) = f `(x)dx.
Если приращение функции ∆f(x) = A*∆x + 0(∆x), где A=const, 0(∆x) – бесконечно малая, более высокого порядка, чем ∆x, то говорят, что f(x) имеет дифференциал в точке x и он равен главной линейной части приращения A*∆x.
Теорема: если f(x) дифференцируема в точке x, то df(x) = f `(x)dx
Доказательство:
∆f(x) = A*∆x + 0 (∆x)
 = A +
= A + 
f `(x) =  =
=  = A, т.е. A = f `(x)
= A, т.е. A = f `(x)
df(x) = f `(x)*∆x
возьмём f(x)= x
dx = x`∆x = ∆x, т.е. ∆x = dx
df(x) = f `(x)dx
из формулы f `(x) = 
41. Производные и дифференциалы высших порядков.
Производной n -го порядка от функции  называется производная от производной (n - 1)-го порядка:
называется производная от производной (n - 1)-го порядка:

Производная второго порядка: 
df(x) = f `(x)dx
d2f(x) = d (df(x)) = d(f `(x)dx) = (f `(x)dx)`dx = f ``(x)dx dx + f `(x)(dx)`dx = f ``(x)(dx)2
f ``f(x) = d(dn-1 f(x))
Формула для вычисления дифференциала n–го порядка
| dn f(x) = f(n) (x) dxn. |
42. Теорема Ферма. Теорема Ролля.
Теорема Ферма: Пусть f(x) непрерывная функция на [a,b], xo принадлежит [a,b] – точка экстремума, существует f `(xo). Тогда f `(xo) = 0
Доказательство: Пусть xo – точка максимума => существует b > 0: f(x) ≤ f(xo). Любой x принадлежит (xo – b, xo + b)
Если x принадлежит (xo – b, xo), то ∆x = x – xo ≤ 0
 =
= 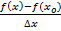 ≥ 0
≥ 0
Если x принадлежит (xo; xo + b), то ∆x ≥ 0
 =
= 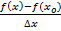 ≤ 0
≤ 0
т.к. существует f `(x), то существует  = f `(xo) ≤ 0
= f `(xo) ≤ 0
существует  = f `(xo) ≥ 0
= f `(xo) ≥ 0
=> f `(xo) = 0.
Теорема Ролля: Если f(x) – непрерывна на отрезке [a,b], f(a) = f(b), f(x) – дифференцируема на (a,b), то существует xo, принадлежащий [a,b]: f `(xo) = 0
Доказательство: т.к. f(x) – непрерывна на [a,b], то по теореме о непрерывных функциях существует максимальное M и минимальное m значение f(x). Если m=M, то f(x)=const. f `(x) = 0.
43. Теорема Лагранжа и следствия из нее. Теорема Коши.
Теорема Лагранжа: Если f(x) – непрерывна на [a,b], f(x) – дифференцируема на (a,b), то существует xo, принадлежащий (a,b): f(b) – f(a) = f `(xo)(b - a)
Следствие 1: Если f `(x) = 0 любой x, принадлежащий [a,b], то f(x) = const.
Следствие 2: Если для любого x, принадлежащего (a,b) значение производной > 0, то эта функция возрастает на интервале (a,b). Если значение производной < 0, то убывает.
Следствие 3: Пусть X - некоторый промежуток, и значения производной на этом промежутке ограничены числом C: |f `(x)| ≤ C. Тогда функция f(x) равномерно непрерывна на данном промежутке.
Теорема Коши: Если f(x), g(x) – непрерывны на [a,b]. f(x), g(x) дифференцируемы на (a,b) g`(x) ≠ 0, любой x принадлежит (a,b), то существует xo, принадлежащее (a,b):  =
= 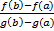
44. Правило Лопиталя.
Раскрытие неопределённостей [  ],[
],[  ] в пределах.
] в пределах.
Теорема: Пусть g(x), f(x) – неопределённости на [a,b] и дифференцируемы на (a,b). Если выполнено одно из условий:
1)  =
=  = 0;
= 0;
2)  =
=  = ∞, причём существует
= ∞, причём существует  < ∞.
< ∞.
То существует 
Замечание 1: Если f `(x) и g`(x) удовлетворяют условию теоремы Лопиталя, то можно повторно применить эту теорему.
Замечание 2: Теорема Лопиталя верна и для случая x --> ∞
45. Возрастание и убывание дифференцируемой функции. Необходимые и достаточные условия.
Поиск по сайту: