Элементы линейной алгебры

1. Операции над матрицами. Свойства операций.

Матрицей, размера n*m называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Операции:

1) Сложение. Складываются матрицы только одного размера. Получается матрица того-же размера.

2) Умножение матрицы на число. Умножать можно любую матрицу на число. Полученная матрица того-же размера.

3) Произведение матриц. Произведение A*B определено, если число столбцов A = числу строк матрицы B.

Свойства:

1) A + B = B + A

2) (A + B) + C = A + (B + C)

3) A + 0 = A

4) α(A + B) = αA + αB

5) α(β*A) = (α β)*A

6) (α + β)*A = α*A + A*β

7) A*0 = 0

8) A*B ≠ B*A

9) (A*B)*C = A*(B*C)

10) (A+B)*C = A*C + B*C

11) α(A*B) = (α*A)*B = A*(α*B)

12) A*E = E; E*A = A E – единичная матрица.

свойства транспонирования:

1) (A^t)^t = A

2) (A + B)^t = A^t + B^t

3) (A*B)^t = B^t * A^t

4) (α*A)^t = α*A^t

2. Определители 2-го и 3-го порядков. Минор и алгебраическое дополнение. Определитель n-го порядка. Свойства определителей.

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

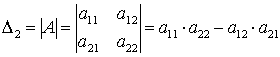
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

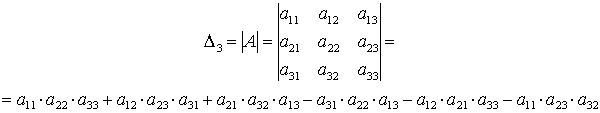
Минором M_ij элемента a_ij называется определитель матрицы, полученной из матрицы A = (a_ij) вычёркиванием i-ой строки и j-го столбца.

Например, есть матрица: Предположим, надо найти минор

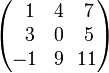
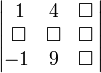
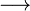
Получаем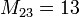

Алгебраическим дополнением A_ij элемента a_ij называется число A_ij = (-1)^i+j * M_ij

Определитель n-ого порядка есть сумма произведений элементов 1 строки на их алгебраические дополнения.

Свойства:

1) Определитель равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

и т.д.

2) |A| = |A^t|

3) Если в определителе поменять местами любые 2 строки (или столбца), то определитель поменяет знак на противоположный.

4) Если в определителе к элементам одной строки прибавить элементы другой строки, умноженные на число, то определитель не изменится.

5) Сумма произведений элементов одной строки на алгебраические дополнения другой строки = 0.

6) |A*B| = |A| * |B|

3. Обратная матрица. Теорема существования обратной матрицы.

Обратной матрицей к квадратной матрице А порядка n называется такая квадратная матрица B порядка n, что A*B = E и B*A = E. Если существует обратная матрица, то она единственна.

B = A^-1 – обратная матрица.

Теорема: Обратная матрица A^-1 для A существует тогда и только тогда, (<=>) когда |A| ≠ 0 (когда A – невырожденная матрица)

Доказательство:

4. Системы линейных уравнений. Матричная запись системы. Формулы Крамера.

Системой m линейных уравнений с n неизвестными называется система вида

AX = B D - расширенная матрица

Формулы Крамера:

Пример:

x₁ + x₂ + x₃ + x₄ = 5,

x₁ + 2x₂ - x₃ + 4x₄ = -2,

2x₁ - 3x₂ - x₃ - 5x₄ = -2,

3x₁ + x₂ +2x₃ + 11 x₄ = 0.

Решение. Главный определитель этой системы

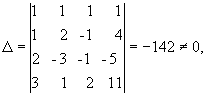
значит, система имеет единственное решение. Вычислим вспомогательные определители ∆ _i (i = 1 - 4), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при x_i, столбцом из свободных членов:

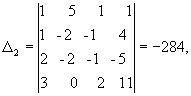
Отсюда x₁ = D ₁/D = 1, x₂ = D ₂/D = 2, x₃ = D ₃/D = 3, x₄ = D ₄/D = -1

5. Однородная система линейных уравнений и свойства ее решений.

Однородной системой m линейных уравнений с n неизвестными называется система вида

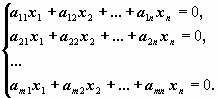
Свойства решений:

Теорема 1. Линейная комбинация решений однородной системы является решением системы.

Теорема 2. Разность двух решений неоднородной системы является решением однородной системы.

Теорема 3. Сумма решения однородной системы с решением неоднородной системы есть решение неоднородной системы.

6. Решение систем методом Гаусса.

Метод Гаусса заключается в последовательном исключении неизвестных с помощью следующих преобразований:

1) Умножение уравнения на число, отличное от нуля.

2) Прибавление к одному уравнению другого, умноженного на число.

3) Перемена местами уравнений.

4) Замена местами неизвестных.

С помощью этих преобразований система сводится к системе трапецеидального вида.

Поиск по сайту: