Алгебры и подалгебры

Всякую функцию типа

будем называть -арной операцией, определенной на множестве . При этом число аргументов называется арностью операции. В частности, при имеем бинарную операцию

.

Опр.3.1.1. Множество вместе с заданной на нем совокупностью операций называется алгеброй . При этом само множество называется носителем алгебры, а совокупность операций – сигнатурой алгебры.

Набор арностей операций из сигнатуры называется типом алгебры.

Множество 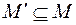называется замкнутым относительно некоторой операции , определенной на , если значения на аргументах из сами принадлежат , т.е.

.

Если замкнуто относительно всех операций из сигнатуры алгебры , то называется подалгеброй алгебры

Пример.

1) Для алгебры .

Так как обе операции бинарные, то тип алгебры . Такая алгебра называется полем действительных чисел.

Очевидно, что есть подалгебра .

2) Пусть задано некоторое множество , а – его булеан. Тогда алгебра ¯ имеет сигнатуру ¯ , а ее тип . Данная алгебра называется булевой алгеброй множеств или алгеброй Кантора. ▲

Если – конечное множество, то бинарные операции могут быть заданы таблицами.

Пример.

1) Рассмотрим квадрат с вершинами в точках , , , и повороты вокруг центра квадрата, переводящие вершины друг в друга. Зафиксируем некоторое направление поворота как положительное. Существует всего 4 различных поворота, переводящих вершины в себя, а именно, повороты на 0, , , радиан. Таким образом, получаем алгебру с носителем , , , и 4 унарными операциями-поворотами . Таблица имеет вид:

Тип алгебры (1, 1, 1, 1). У этой алгебры нет подалгебр.

2) Рассмотрим множество поворотов с бинарной операцией: – композицией преобразований. Тогда 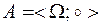есть алгебра поворотов с носителем и сигнатурой, состоящей из одной операции . Тип алгебры (2). Ее таблица Кэли имеет вид:

◦

Множество 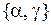образует подалгебру алгебры :

◦

▲

Поиск по сайту: