АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Группы и подгруппы

Читайте также:
  1. А. Группы приказов.
  2. Августа 1992 года Тёрнеру позвонил Брюс Пэйн и сказал, что он уволен из группы.
  3. Алекс, Стивенсон и часть группы заняли свои места на диванчиках по обе стороны от экрана, на котором сейчас было изображение эмблемы передачи.
  4. АМОРТИЗАЦИОННЫЕ ГРУППЫ И ПОДГРУППЫ
  5. Анализ времён распространения гаплогруппы R1b1a2
  6. Большие группы
  7. Большие социальные группы и психологические механизмы их саморегуляции
  8. Взаимодействие индивида и малой группы
  9. Взаимосвязь личности и группы.
  10. Виды дисперсий в совокупности,разделенной на группы
  11. Витамины группы D
  12. Витамины группы В

Опр.3.3.1. Пусть – непустое множество с бинарной операцией . Тогда, если выполняются следующие условия:

1) операция – ассоциативна;

2) в множестве имеется единичный элемент ;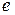

3) для : ;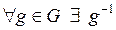

то множество называется группой.

 

Таким образом, группа – это обратимый моноид. Число элементов в группе называется ее порядком.

Группа, в которой операция – коммутативна, называется абелевой. Если есть , то группа называется циклической.

Пример.

1) 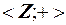– абелева группа;

2) – абелева группа;

3) Пусть – множество всех перестановок -го порядка . Тогда – симметрическая группа, где – операция композиции перестановок. ▲

 

Опр.3.3.2. Подмножество 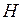группы называется подгруппой, если 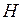само образует группу.

 

Очевидно, что 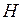должно содержать единицу .

 

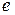Опр.3.3.3. Если 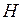есть подгруппа и , то множество

называется левым смежным классом для а. Обозначим его как . Аналогично вводится и правый смежный класс: .

 

Свойства смежных классов и подгрупп по подгруппе Н:

I. Смежные классы задают разбиение группы .

II. (теорема Лагранжа) Порядок конечной подгруппы 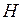является делителем порядка конечной группы .

III. Если порядок есть простое число, то у группы нет нетривиальных подгрупп.

IV. Число различных смежных классов равно частному .

Алгебры с различными типами являются различными. Однако, если алгебры имеют один тип, то они могут быть похожи друг на друга. Степень схожести характеризуется понятием «морфизм».

 

Опр.3.3.4. Пусть имеются две алгебры

и .

Тогда отображение , удовлетворяющее условию

называется гомоморфизмом.

Если гомоморфизм взаимно-однозначный, то он называется изоморфизмом. Если установлен изоморфизм алгебр, то, получив некоторые соотношения в алгебре А, можно их распространить на алгебру В.

 

Теорема 3.3.1. Любая подгруппа с единицей (моноид) изоморфна некоторой полугруппе преобразований носителя М.

 

Теорема 3.3.2. (теорема Кэли) Всякая конечная группа изоморфна группе подстановок на множестве ее элементов.

 

Замечание: В группе при любом количестве «умножений» не теряется информация об исходном элементе. В подгруппе это не всегда так.

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)