Виды дисперсий в совокупности,разделенной на группы

Правило сложения:

Если данные представлены в виде аналитической группировки, то можно определить 3 показателя колеблемости признака в совокупности.

1) Общая дисперсия измеряет вариацию признака всей совокупности под влиянием всех факторов,обусловивших эту вариацию.

2) Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающее под влиянием признака-фактора, положенного в основании группировки

3) Внутригрупповая дисперсия отражает случайную вариацию,т.е часть вариации,происходящую под влиянием неучтенных факторов и не зависящую от признака фактора

=

3)* Средняя из внутригрупповых дисперсий. ПО совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий

=

Правило сложения дисперсий:

Эмпирический коэффициент детерминации –

соотношение межгрупповой и общей дисперсии, показывает какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки.

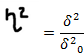
– эмпирическое корреляционное отношение характеризует влияние признака, положенного в основании группировки на вариацию результативного признака

и обозначается «эта»

Эта=0 –группировочный признак не оказывает влияние на результативный

Эта=1 результативный признак изменяется только в зависимости от признака,положенного в основании группировки, а влияние прочих факторных признаков=0

Правило сложения дисперсий для доли признака:

1. Внутригрупповая дисперсия:

2. Средняя из внутригрупповых дисперсий:

3. Межгрупповая дисперсия:

4. Общая дисперсия:

= *

Поиск по сайту: