 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лекция № 3. Показатели центра распределения: ü Мода ü Медиана ü Средняя Показатели степени вариации: ü Вариационный размах
Показатели центра распределения:
ü Мода
ü Медиана
ü Средняя
Показатели степени вариации:
ü Вариационный размах
ü Среднее линейное отклонение
ü Дисперсия
ü Среднее квадратическое отклонене
ü Коэффициент вариации
Показатели вариации Показатели типа (формы) распределения:
ü Структурные характеристики
ü Показатели ассиметрии и эксцесса
ü Кривые распределения
Мода (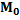
) – значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. один из вариантов признака повторяется чаще, чем другие.
= 
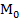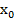+i* 
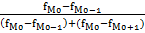
ü 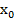-нижняя граница интервала, содержащего моду
ü
| Частоты (частости) модального, предмодального и послемодального интервалов соответственно. |
−величина шага
ü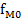 
ü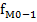 
ü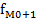 
- При нечетном числе вариантов:
= 
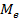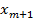
- При четном числе вариантов: =
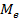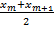
Медиана (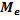
) – величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда, т.е.это вариант, который делит ряд распределения на 2 равные по объему части.
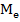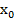= +i*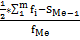 
ü №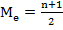 
ü 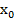и i – соответственно, нижняя граница и величина медианного интервала, соответственно.
ü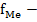 
частота медианного интервала
ü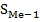 
- накопленная частота предмедианного интервала
ü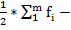 
половина объема распределения
- Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функцию средней величины для неоднородной совокупности.
Положение медианы в ряду распределения определяется ее номером:
, где n – число единиц совокупности
Формула, по которой смотрится ассиметрия ряда в рамках 1 единицы:
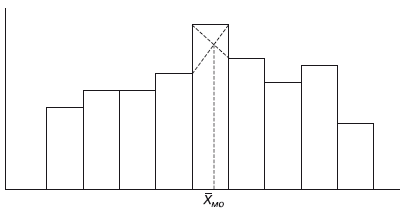
Построение моды:
1) Строится гистограмма (по оси x – варианты ряда (границы интервалов), по оси y – частоты)
2) Выбирается самый высокий столбец
3) Правый и левый верхние его концы соединяют с соседними столбцам
4) Из точки, получившейся при пересечении двух линий, опускают вниз прямую, это и есть мода.
Мода – график – гистограмма.
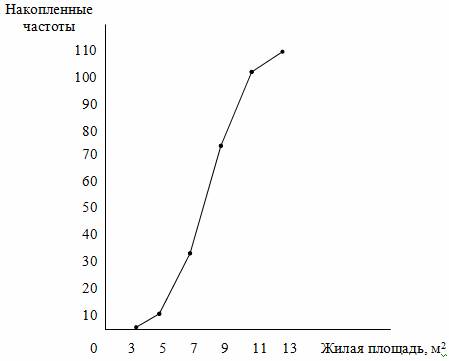
Медиана – график – кумулята. Медиана строится на основе ряда кумулятивных или накопленных частот. (по оси x – откладывают значения признака).
Абсолютные:
· Размах вариации
· Среднее линейное отклонение
· Дисперсия
· Среднее квадратическое отклонение
Показатели вариации (абсолютные и относительные) Относительные:
(отношение абсолютных показателей к средней арифметической или медиане)
Как выбрать, соотношение средней или медианы? – Если совокупность однородная, то сред.арифметическая, если неоднородная, то медиана.
· Коэффициенты оссиляции, вариации
· Относительное линейное отклонение
АБСОЛЮТНЫЕ:
- Вариационный размах: R =
- 
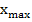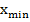
1. Среднее линейное отклонение:
a) Невзвешенная средняя: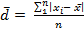 
b) Взвешенная средняя: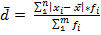 
- Дисперсия - это средний квадрат отклонений индивидуальных значений признака от средней величины.
a) Простая (невзвешенная):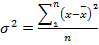 
b) Сложная (взвешенная):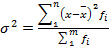 
- Среднее квадратическое отклонение – это корень квадратный из дисперсии.
a) Простая (невзвешенная):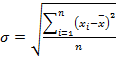 
b) Сложная (взвешенная):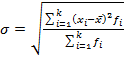 
ОТНОСИТЕЛЬНЫЕ:
1. Коэффициент осцилляции: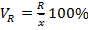 
2. Линейный коэффициент вариаци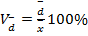и: 
или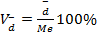 
3. Коэффициент вариации: 
Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Способ отсчета от условного нуля или способ моментов:
= 
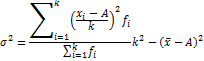
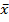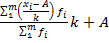
A – условный нуль, в качестве которого используются середины интервала, обладающего наибольшей частотой.
k – шаг интервала
ü Этот способ используется только в том случае, если ряд обладает равными интервалами.
Поиск по сайту: