 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической.
Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Количественные критерии оценки тесноты связи (по Чеддону):
| Величина коэффициента корреляции | Характер связи |
| до│±0,3│ | практически отсутствует |
| │±0,3│-│±0,5│ | слабая |
| │±0,5│-│±0,7│ | умеренная |
| │±0,7│-│±1,0│ | сильная |
Оценка линейного коэффициента корреляции:
| Значение линейного коэф.связи | Характер связи | Интерпретация связи |
| r=0 | отсутствует | |
| 0<r<1 | прямая | С увеличением x увеличивается y |
| -1<r<0 | обратная | С увеличением х уменьшается у |
| r=1 | функциональная | Каждому значению факторного признака строго соответствует 1 значение результативного признака |
По аналитическому выражению связи бывают прямолинейные(линейные) и нелинейные(криволинейные)
Если статистическая связь между явлениями приближенно выражена уравнением прямой линии, то ее называют линейной связью
Если же связь выражена уравнением какой-либо кривой линии, то такую связь называют нелинейной или криволинейной.
Метод приведения парал.данных:
Он основан на сопоставлении двух или нескольких рядов статистических величин. При отсутствии тесной связи наблюдается беспорядочное расп-е точек на графике. Чем сильнее связь между пр-ми, тем сильнее будут группированы точки вокруг определенной линии, выражающей форму связи
Ломаная регрессия:
Задача корреляц.метода-это количественное опрелеление тесноты связи между пр-ми. Регрессионный метод закл.в определении аналитического выражения связи,ее формы. Корреляц.-регрессивный анализ включет в себя:
1)измерение направления связи 2)установление аналитического выражения
Аналитическая связь описывается уравнениями:
1.прямой 
2.гиперболы 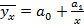
3.параболы 
Если результативный и факторный признаки возрастают одинаково примерно в арифм.прогрессии,то связь между ними линейная,а при обратной связи гиперболическая
Если факторный признак увеличивается в арифм.прогрессии,а результативный значительно быстрее,то использ.связь параболическая
Метод наименьших квадратов:
Оценка параметров уравнения регрессии осущ.на основе этого метода

С-ма уравнений для нахождения параметров линейной парной регрессии:

n-объем исследуемой совокупности
 -показывает усредненное влияние на результативный признак как неучтенных факторов
-показывает усредненное влияние на результативный признак как неучтенных факторов
 -показывают насколько изменилось в среднем значение результ.признака при изменении факторного на единицу его собственного измерения
-показывают насколько изменилось в среднем значение результ.признака при изменении факторного на единицу его собственного измерения
1)Если оба признака x и у распол.в возраст.порядке,а частоты(f)сосредоточены по диагонали сверху вниз направо,то можно судить о прямой связи между пр-ми, в противном случае об обратном
2)Чем ближе частоты располаг.к одной из диагоналей,тем теснее связь
3)Если в расположении частот нет системности,то можно судить об отсутствии связи
Считая,что зависимость описывается уравнением прямой,коэф.  определяются из системы нормальных уравнений:
определяются из системы нормальных уравнений:

Если связь между пр-ми криволинейная и описыв.уравнением параболы 2ого порядка,то с-ма нормал.уравнений имеет вид:

Оценка обратной зависимости между х и у осуществляется на основании уравнения гиперболы

Изучение связи между 3 и более связанными между собой пр-ми носит название множественной регрессии
Поиск по сайту: