 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Группоиды и полугруппы
Далее рассмотрим различные алгебры с одной операцией.
Опр.3.2.1. Алгебра вида 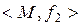 , где
, где  – некоторая бинарная операция
– некоторая бинарная операция 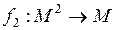 называется группоидом. Если
называется группоидом. Если  – операция типа умножения, то группоид называется мультипликативным, а если тип сложения – аддитивным.
– операция типа умножения, то группоид называется мультипликативным, а если тип сложения – аддитивным.
Для бинарной операции удобно ввести некоторые общие обозначения:
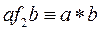 .
.
Опр.3.2.2. Группоид называется коммутативным, если
 (3.2.1)
(3.2.1)
и ассоциативным, если
 . (3.2.2)
. (3.2.2)
Важным примером ассоциативного группоида является множество отображений с композицией. Примером некоммутативного группоида является множество матриц с операцией – матричное умножение. Пример не ассоциативного группоида – булеан 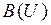 с декартовым произведением
с декартовым произведением 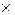 .
.
Опр.3.2.3. Элемент 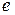 группоида
группоида 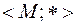 называется единичным для операции *, если выполняются равенства
называется единичным для операции *, если выполняются равенства
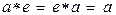 . (3.2.3)
. (3.2.3)
Для мультипликативных группоидов 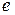 есть 1, а для аддитивных – 0.
есть 1, а для аддитивных – 0.
Замечание: Вообще-то возможно введение левого или правого единичных элементов. Однако, если в группоиде есть  и
и 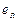 , то они совпадают.
, то они совпадают.
Опр.3.2.4. Группоид с ассоциативной операцией * называется полугруппой. Полугруппа с единицей называется моноидом.
Пример.
1) 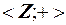 – полугруппа,
– полугруппа,
т.к.  для любых чисел из
для любых чисел из 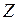 .
.
2)  – группоид, но не полугруппа,
– группоид, но не полугруппа,
т.к. 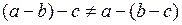 . ▲
. ▲
Рассмотрим следующий важный пример полугрупп.
Пусть имеется множество символов  , которые назовем алфавитом. Тогда некоторая упорядоченная совокупность символов образует слово. Для удобства вводится в качестве отдельного символа пробел
, которые назовем алфавитом. Тогда некоторая упорядоченная совокупность символов образует слово. Для удобства вводится в качестве отдельного символа пробел  . Рассмотрим множество всех символов
. Рассмотрим множество всех символов  . Введем над символами следующую бинарную операцию:
. Введем над символами следующую бинарную операцию:
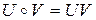 . (3.2.4)
. (3.2.4)
Ее называют конкатенацией (другие названия - сцепление, приписывание, слияние). Очевидно, что эта операция–слияние не коммутативна, но ассоциативна. Следовательно, наш группоид 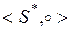 является полугруппой. Она называется свободной полугруппой. Безусловно, можно выделить не все слова, а только их часть
является полугруппой. Она называется свободной полугруппой. Безусловно, можно выделить не все слова, а только их часть 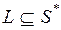 . Такое подмножество удобно называть языком.
. Такое подмножество удобно называть языком.
Понятие языка можно ввести на любом множестве, в частности, на двухэлементном множестве  . На языке можно вводить различные грамматики типа
. На языке можно вводить различные грамматики типа 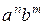 ,
, 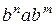 и т.п. Развитие такой алгебраической теории приводит нас к теории автоматов.
и т.п. Развитие такой алгебраической теории приводит нас к теории автоматов.
Всякую полугруппу можно получить из свободных полугрупп путем задания так называемых определяющих соотношений
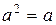 ,
,  и т.п.
и т.п.
Из любого слова, используя определяющие соотношения, можно получить эквивалентные слова.
Намного более сложной является обратная задача – установление эквивалентности двух слов. Эта задача приводит к теории алгоритмов.
Поиск по сайту: