ОСНОВЫ АЛГЕБРЫ ЛОГИКИ

Все устройства МП состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: Истинности и ложности выска­зывания. В соответствии с такой двоичной природой высказываний их условились называть ЛОГИЧЕСКИМИ ДВОИЧНЫМИ ПЕРЕМЕННЫМИ и обозначать 1 в случае истинности и 0 в случае ложности. Примерами логических переменных являются высказывания:

А="Земля плоская", В="Парта черная". На основании этих высказы­ваний можно записать А=0; В=1, т.к. высказывание А ложно, а высказывание В истинно.

Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями.

Формализация и преобразование связей между логическими переменными осуществляется в соответствии с правилами АЛГЕБРЫ ЛОГИКИ называемой АЛГЕБРОЙ БУЛЯ.

Две логические переменные А и В принимающие значения 0 или 1, могут образовывать логические функции. Для описания логической функции используют, так называемую, таблицу истинности, в левых колонках которой отображают все возможные значения логических переменных, а справа соответствующие значения функции. Таким образом, каждая строка таблицы соответствует определенному состоянию функции или устройства, ее реализующего.

Наибольший практический интерес представляют функции отрицания, логического умножения и логического сложения..

1.Логическое отрицание НЕ переменной А есть логическая функция Х, которая истинна, когда А ложно, и наоборот. Инвертор.

_ Х = А	Графически функция НЕ обозначается в виде круга возле вывода (МЭК-117-15)(ГОСТ 2.743-91):
A	X	_ А ┌───┐ Х = А ────┤ 1 о───── или └───┘	_ А ┌───┐ Х = А реже ────о 1 ├───── └───┘
		По американской спецификации milspec:

A├────────┐ ┌───────┐ o +Eп

│ └───────┘ └─────── X│ ┌┴┐

└────────────────────────────────> t │ │ │ R

X│ ┌───────┐ ┌─────── V └┬┘

├────────┘ └───────┘ ┌──────/────┴───>

└────────────────────────────────> t ─┴─

2.Логическое умножение И двух переменных А и В есть логическая функция Х, которая истинна только тогда, когда одновременно истинны обе входные переменные. Кроме того функцию И называют КОНЪЮНКЦИЕЙ.

X=A*B или X=A/\B	Графически функция И обозначается в виде значка & внутри элемента
A	B	X		A ┌────┐ ────┤ & │ Х = А /\ B = A * B B │ ├─────────────────── ────┤ │ └────┘
				По американской спецификации milspec: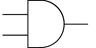

A│ ┌───┐ ┌───────┐ +Eп A B X

├──┘ └─────────┘ └─────── o────/────/───┬───>

└────────────────────────────────> t ┌┴┐

B│ ┌───┐ ┌───────┐ │ │R

├────────┘ └──────┘ └──── └┬┘

└────────────────────────────────> t ─┴─

X│ ┌────┐

├───────────────────┘ └───────

└────────────────────────────────> t

3.Логическая сумма ИЛИ двух переменных А и В есть логическая функция Х, которая истинна, когда истинна хотя бы одна из входных переменных. Кроме того функцию ИЛИ называют ДИЗЪЮНКЦИЕЙ.

X=A+B или X=A\/B	Графически функция ИЛИ обозначается в виде значка 1 внутри элемента
A	B	X		A ┌────┐ ────┤ 1 │ Х = А \/ B = A + B B │ ├─────────────────── ────┤ │ └────┘
				По американской спецификации milspec: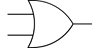

A│ ┌───┐ ┌───────┐ +Eп A X

├──┘ └─────────┘ └─────── o─────┬───/───┬───>

└────────────────────────────────> t │ │

B│ ┌───┐ ┌───────┐ │ B │

├────────┘ └──────┘ └──── └───/───┤

└────────────────────────────────> t ┌┴┐

X│ ┌───┐ ┌───┐ ┌──────────┐ │ │R

├──┘ └─┘ └───┘ └──── └┬┘

└────────────────────────────────> t ─┴─

Три рассмотренных функции позволяют реализовать любую логическую комбинацию. Более того, сочетание одной из функций И либо ИЛИ с функцией НЕ также позволяет реализовать любую сложную функцию. Например, реализуем функцию ИЛИ с помощью элементов И и НЕ.

_

A ┌───┐ A ┌───┐ _ _ ─ ─── ─

────┤ o─────┤ & │ A * B ┌───┐ A * B = A + B

└───┘ _ │ ├───────┤ o──────────────

B ┌───┐ B │ │ └───┘

────┤ o─────┤ │

└───┘ └───┘

Рассмотрим еще три функции получившие широкое применение в цифровой технике:
4. И-НЕ "Штрих Шеффера"

A	B	X		A ┌────┐ _____ ────┤ & │ Х = A * B B │ о────────── ────┤ │ └────┘
				По американской спецификации milspec: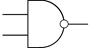

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X├───────────────────┐ ┌───────

│ └────┘

└────────────────────────────────> t

5. ИЛИ-НЕ "Стрелка Пирса"

A	B	X		A ┌────┐ ______ _____ ────┤ 1 │ Х = А \/ B = A + B B │ о─────────────────── ────┤ │ └────┘
				По американской спецификации milspec: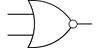

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X├──┐ ┌─┐ ┌───┐ ┌────

│ └───┘ └───┘ └──────────┘

└────────────────────────────────> t

Две рассмотренные функции интересны тем, что являются достаточными для построения любой сложной функции, т.к. содержат в своем составе функцию И либо ИЛИ и инвертор.

┌───┐ _____ _ ┌───┐ _____ _

A ┌─┤ & │ A * A = A 1 o──┤ & │ A * 1 = A

────┤ │ o────────── │ o──────────

└─┤ │ A ─────┤ │

└───┘ └───┘

6. "ИСКЛЮЧАЮЩЕЕ ИЛИ" или СУММИРОВАНИЕ ПО МОДУЛЮ 2

A	B	X		A ┌────┐ _ _ ────┤ =1 │ Х = A # B = AB + AB = B │ о────────────────────── ────┤ │ ───── ─ ─ ─ └────┘ = AB + A B
				По американской спецификации milspec:

A│ ┌───┐ ┌───────┐

├──┘ └─────────┘ └───────

└────────────────────────────────> t

B│ ┌───┐ ┌───────┐

├────────┘ └──────┘ └────

└────────────────────────────────> t

X│ ┌───┐ ┌───┐ ┌──┐ ┌──┐

├──┘ └─┘ └───┘ └────┘ └────

└────────────────────────────────> t

_

A ┌───┐ A 1 o ┌───┐ A

─────┤=1 ├──── Повторитель A └──┤=1 ├──── Инвертор

┌──┤ │ ───────┤ │

─┴─ └───┘ └───┘

.

Рассмотрим наиболее распространенные правила алгебры логики на примерах с минимальным количеством переменных:

1: X = A * 0 = 0 \

│

2: X = A * 1 = A │ законы

>

3: X = A * A = A │ конъюнкции

_ │

4: X = A * A = 0 /

5: X = A + 0 = A \

│

6: X = A + 1 = 1 │ законы

>

7: X = A + A = A │ дизъюнкции

_ │

8: X = A + A = 1 /

=

9: X = A = A двойная инверсия

10: X = A * B = B * A \ переместительный

>

11: X = A + B = B + A / закон

12: X = (A * B) * C = A * (B * C) \ сочетательный

>

13: X = (A + B) + C = A + (B + C) / закон

14: X = A * (B + C) = AB + AC \ закон дистрибутивности

>

15: X = A + BC = (A + B) * (A + C) / или распределительный

16: X = A + AB = A { A + BA = A (1 + B) } \

│

17: X = A (A + B) = A > законы

_ _ │ погло-

18: X = A + AB = A + B { (1 + A) (A + B) = A + B } / щения

_

19: X = AB + AB = B \ законы

_ > склеивания

20: X = (A + B) (A + B) = B /

__ _ _

21: X = AB = A + B \ правила Де Моргана

_____ _ _ > или

22: X = A + B = A * B / законы инверсии

.

Пример: Задана в виде таблицы истинности логическая функция Y трех переменных A,B,C.

┌───┬───┬───┬───┐ Функция принимает единичное значение при

│ А │ B │ C │ Y │

├───┼───┼───┼───┤ следующих произведениях переменных:

│ 0 │ 0 │ 0 │ 0 │ _ _

├───┼───┼───┼───┤ ABC, ABC, ABC

│ 0 │ 0 │ 1 │ 0 │

├───┼───┼───┼───┤ Каждое из произведений переменных для ║

│ 0 │ 1 │ 0 │ 0 │ ║

├───┼───┼───┼───┤ которых значение функции истинно, носит ║

│ 0 │ 1 │ 1 │ 1 │ ║

├───┼───┼───┼───┤ название МИНТЕРМА. ║

│ 1 │ 0 │ 0 │ 0 │

├───┼───┼───┼───┤ В соответствии с этим, функция может

│ 1 │ 0 │ 1 │ 0 │

├───┼───┼───┼───┤ быть записана в виде уравнения:

│ 1 │ 1 │ 0 │ 1 │ _ _

├───┼───┼───┼───┤ Y = ABC + ABC + ABC

│ 1 │ 1 │ 1 │ 1 │

└───┴───┴───┴───┘

Если при такой записи каждое слагаемое содержит произведения всех переменных или их отрицаний, то такую форму представления функции называют СОВЕРШЕННОЙ ДИЗЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ или ПЕРВОЙ СТАНДАРТНОЙ ФОРМОЙ. Точно так же можно выделять ложные (нулевые) значения функции. Если функция дана в виде произведения (конъюнкции) сумм переменных или их отрицаний, то такую форму представления функции называют СОВЕРШЕННОЙ КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ или ВТОРОЙ СТАНДАРТНОЙ ФОРМОЙ.

A ┌──┐ ┌─────┐ ┌─────┐ Для схемной реализации

───────┬─────┬─┤ о──┤ & │ │ 1 │

B │ │ └──┘ │ │ │ │ полученной функции

─────┬─┼───┬─┼───────┤ ├───┤ │

C │ │ │ │ │ │ │ │ потребуется:

───┬─┼─┼─┬─┼─┼───────┤ │ │ │

│ │ │ │ │ │ ├─────┤ │ │ 3 схемы, выполняющие

│ │ │ │ │ └───────┤ & │ │ │

│ │ │ │ │ │ │ │ │ Y функцию 3И,

│ │ │ │ └─────────┤ ├───┤ ├───

│ │ │ │ ┌──┐ │ │ │ │ 1 схема 3ИЛИ и

│ │ │ └─────┤ о──┤ │ │ │

│ │ │ └──┘ ├─────┤ │ │ 2 схемы НЕ.

│ │ └─────────────┤ & │ │ │

│ └───────────────┤ ├───┤ │

└─────────────────┤ │ │ │

└─────┘ └─────┘

Пользуясь правилами алгебры логики упростим полученную функцию.

_ _ _ _ _ _

Y = ABC + ABC + ABC = ABC + AB (C + C) = ABC + AB = B (AC + A) =

_

= (правило 15) = B (A + A) (C + A) = B (C + A) = BC + AB

Полученная функция и ее схемная реализация значительно проще исходных.

A ┌───┐ ┌───┐ A ┌───┐ ┌───┐

─────┤ & ├───┤ 1 │ ─────┤ & o───┤ & │

B ┌─┤ │ │ │ Y B ┌─┤ │ │ │ Y

───┤ ├───┤ │ ├──── ───┤ ├───┤ │ o────

C └─┤ & ├───┤ │ C └─┤ & o───┤ │

─────┤ │ │ │ ─────┤ │ │ │

└───┘ └───┘ └───┘ └───┘

─── ─── ──

Y = Y = AB + BC = AB * BC - для построения схемы на одинаковых элементах

Можно было представить ту же самую функцию в СОВЕРШЕННОЙ

КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМЕ в виде произведения сумм:

_ _ _ _ _

Y = (A + B + C) (A + B + C) (A + B + C) (A + B + C) (A + B + C)

Такая запись слишком сложна для минимизации и реализации.

Разработан метод минимизации логических функций, как бы автоматизирующий процедуру поиска "склеивающихся слагаемых - метод КАРТ КАРНО.

Карта Карно - это таблица имеющая ячейки для всех возможных минтермов функции. Можно построить карты Карно для функций, минтермы которых содержат два, три и более переменных (обычно не более 5...6). Составим карту Карно для функции 2-х переменных: Вдоль верхней грани проставлены возможные значения

_

A A переменной А, вдоль левой боковой грани -

┌────┬────┐

│ │ _ │ возможные значения переменной В. В каждой

B │ AB │ AB │

├────┼────┤ клетке изображают один из возможных мин-

_ │ _ │ _ _│

B │ AB │ A*B│ термов: AB, AB, AB, AB. Если какой-то из

└────┴────┘

этих минтермов в совершенной дизъюнктивной

нормальной форме записи функции присутствует, то в соот-

ветствующей клетке карты Карно ставится "1",если нет - то "0".

Составим карты Карно для функций 3-х и 4-х переменных:

-- - - -- - -

AB AB AB AB AB AB AB AB

┌────┬────┬────┬────┐ ┌────┬────┬────┬────┐

- │ ---│ - -│ -│ --│ -- │----│- --│ --│ ---│

C │ ABC│ ABC│ ABC│ ABC│ CD │ABCD│ABCD│ABCD│ABCD│

├────┼────┼────┼────┤ ├────┼────┼────┼────┤

│ -- │ - │ │ - │ - │--- │- - │ - │ -- │

C │ ABC│ ABC│ ABC│ ABC│ CD │ABCD│ABCD│ABCD│ABCD│

└────┴────┴────┴────┘ ├────┼────┼────┼────┤

│-- │- │ │ - │

Склеивание осуществляется между CD │ABCD│ABCD│ABCD│ABCD│

├────┼────┼────┼────┤

теми минтермами, которые запи- - │-- -│- -│ -│ - -│

CD │ABCD│ABCD│ABCD│ABCD│

саны в виде "1" в соседних клет- └────┴────┴────┴────┘

ках карты (по вертикали или горизонтали). Соседними считаются

клетки крайнего левого и правого, верхнего и нижнего рядов

(можно представить карту как развертку цилиндра). Два минтер-

ма, находящиеся в соседних клетках можно представить в виде

одного логического произведения переменных, число которых на

одну единицу меньше, чем в каждом из соседних минтермов, при-

чем в произведении остаются общие для обоих минтермов сомножи-

тели. Если соседними окажутся сразу 4 минтерма с "1" то такую

группу можно заменить произведением переменных, число которых

меньше, чем в каждом минтерме, уже на два. Учитывая, что

А + А +...+ А = А, одну единицу, изображающую минтерм, можно

объединять пары несколько раз.

Используя метод карт Карно минимизируем рассмотренную в

примере функцию. Единица, изображающая минтерм АВС входит сра-

-- - -

AB AB AB AB зу в два объединения, обозначенные

- ┌────┬────┬────┬────┐

C │ 0 │ 0 │ 1 │ 0 │ a и b. Объединение a отражает

├────┼────┼─a│─┼────┤ _

C │ 0 │ 1 ─ 1 │ 0 │ "склеивание" минтермов АВС и АВС

└────┴────b────┴────┘ _ _

АВС + АВС = АВ (С + С) = АВ

_

объединение b отражает склеивание минтермов АВС и АВС

_ _

ABC + ABC = BC (A + A) = BC

В результате проведенных операций "склеивания" из трех минтермов, входящих в функцию и являющихся конъюнкцией трех переменных, остались лишь слагаемые АВ и ВС.

Отсюда: Y = AB + BC.

Поиск по сайту: