АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение некоторых задач алгебры матриц

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  3. I. Решение логических задач средствами алгебры логики
  4. I. Розв’язати задачі
  5. I. Ситуационные задачи и тестовые задания.
  6. II. Основные задачи и функции
  7. II. Решение логических задач табличным способом
  8. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  9. II. Цель и задачи государственной политики в области развития инновационной системы
  10. III. Разрешение споров в международных организациях.
  11. III. Решение логических задач с помощью рассуждений
  12. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)

Перейдем к конкретным задачам.

ЗАДАЧА 3.1. Для матриц А, В и С проверить выполнение следующих тождеств: (А ∙ В)∙ С = А ∙(В ∙ С) и (А Т+ В) С = А Т∙ С + В ∙ С. Решение на рис.3.20.

ЗАДАЧА 3.2. Упростить выражение ∆А-3∙∆В+2∙ х –10, где ∆А и ∆В - определители матриц А и В соответственно.

На рисунке 3.21 показано, как можно решить эту задачу, воспользовавшись символьными операциями MathCAD.

ЗАДАЧА 3.3. Проверить, является ли матрица симметрической (АТ=А). Решение приведено на рис.3.22.

ЗАДАЧА 3.4. Проверить, является ли матрица ортогональной (если | A |= det A ≠0 и АТ=А-1).

Для решения этой задачи необходимо вычислить определитель заданной матрицы, и убедиться в том, что он не равен нулю. Затем транспонировать исходную матрицу и найти обратную к ней. Если визуально сложно убедиться в том, что транспонированная матрица равна обратной, можно вычислить их разность. В результате должна получиться нулевая матрица (рис.3.23).

ЗАДАЧА 3.5. Проверить, является ли матрица А идемпотентной (А 2 =А). Показать, что матрица В=2А-Е, где Е – единичная матрица, инволютивна (А 2 =Е, где Е – единичная матрица).

Для того, чтобы выяснить, является ли матрица А идемпотентной, ее необходимо возвести в квадрат и сравнить с исходной. В формировании матрицы В участвует единичная матрица, которую можно получить при помощи описанной выше функции identity(n). Определить, является ли матрица В инволютивной, можно, сравнив ее с единичной матрицей. Подробно решение задачи приведено на рис. 3.24.

Рисунок 3.20. Решение задачи 3.1

Рисунок 3.21. Решение задачи 3.2

Рисунок 3.22. Решение задачи 3.3

рабочего документа, содержащий решение поставленной задачи.

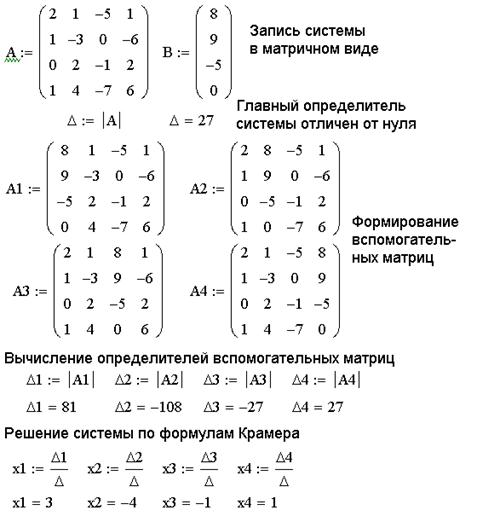
Рисунок 3.26. Решение системы линейных уравнений по формулам Крамера

ЗАДАЧА 3.8. Решить систему линейных уравнений из задачи 3.7 методом обратной матрицы.

Метод обратной матрицы: для системы из n линейных уравнений с n неизвестными A∙x=b, при условии, что определитель матрицы А не равен нулю, единственное решение можно представить в виде x=A-1∙b (вывод формулы см. в задаче 3.6). Итак, для того, чтобы решить систему линейных уравнений методом обратной матрицы, необходимо выполнить следующие действия:

· сформировать матрицу коэффициентов и вектор свободных членов заданной системы;

· решить систему, представив вектор неизвестных как произведение матрицы, обратной к матрице системы и вектора свободных членов (рис.3.27).

Рисунок 3.27. Решение системы линейных уравнений методом обратной матрицы

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)