Трансцендентные уравнения

Уравнение, в котором неизвестное входит в аргумент трансцендентных функций (трансцендентные функции – аналитические функции, не являющиеся алгебраическими, например показательные, логарифмические, тригонометрические и т. д.), называется трансцендентным уравнением.

Рассмотрим применение функции root(F(x), x) для решения трансцендентных уравнений.

ЗАДАЧА 7.13.5. Найти решение уравнения: .

Выражение, стоящее в левой части уравнения, можно представить в виде разности двух функций f (x)– g (x)=0, где , .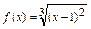

Следовательно, f (x)= g (x), а точка, в которой графики этих функций пересекаются, является графическим решением уравнения. Итак, для решения заданного уравнения (рис. 5.8) выполним следующую последовательность действий:

· введем функции f (x) и g (x);

· определим интервал изоляции корня;

· зададим начальное значение х;

· найдем решение при помощи функции root(f(x)–g(x), x).

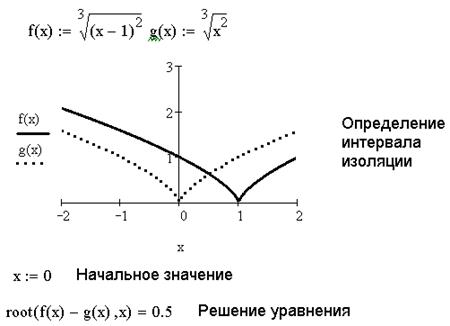
Рис. 7.13.8. Решение трансцендентного уравнения

ЗАДАЧА 7.13.6. Найти корни уравнения f (x)=0.

На рис. 7.13.9. видно, что график функции f (x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня. Для решения этой задачи воспользуемся тем, что функцию root(f(x), x) можно записать в виде:

root(F(x), x, a, b) – возвращает с заданной точностью значение переменной x, при котором выражение F(x) равно нулю, a и b – пределы интервала изоляции корня.

Понятно, что при такой форме записи функции нет необходимости задавать начальное значение x, так как оно определено в интервале [a,b].

Обратите внимание на последнее обращение к функции root на рис. 5. 11. MathCAD выдал сообщение об ошибке: «Значения на обоих концах интервала должны иметь противоположные знаки». Произошло это потому, что интервал изоляции задан неверно. На графике видно, что на концах этого интервала функция знак не меняет.

Рис. 7.13.9.. Вычисление корней трансцендентного уравнения

Поиск по сайту: