Основные тождества алгебры множеств

Основные понятия теории множеств. Способы задания множеств.

Под множеством будем понимать совокупность определённых вполне различаемых объектов, рассматриваемых как единое целое, это понятие – фундаментально. Для обозначения конкретных множеств используются заглавные буквы с индексом или без (A, X1, Х2), элементы множеств обозначаются строчными буквами (а, х1, х2). Принадлежность элемента множеству обозначается символом ∈. Множества бывают конечными и бесконечными. Конечные множества – множества, в которых число элементов конечно. Бесконечные множества – бесконечное число элементов.

Множества задаются двумя способами: перечислением и описанием. Задание перечислением – перечисление всех элементов, составляющих множество. Он удобен для задания конечных множеств с небольшим количеством элементов и для задания множеств типа {2, 4, 6, 8…}.

Описательный способ задания множества состоит в том, что указывается характерное свойство, которым обладают все элементы множества.

Элементы множества – отдельные объекты, из которых состоит множество. Считают, что множество задано своими элементами, т.е. множество задано, если о любом объекте можно сказать: принадлежит он этому множеству или не принадлежит. Задавать множество можно следующими способами:

1) Если множество конечно, то его можно задать перечислением всех его элементов. Так, если множество А состоит из элементов 2, 5, 7, 12, то пишут А = {2, 5, 7, 12}. Количество элементов множества А равно 4, пишут n(А) = 4.

Но если множество бесконечно, то его элементы нельзя перечислить. Трудно задать множество перечислением и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества.

Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.

Операции над множествами. Основные тождества алгебры множеств.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).

Свойства перестановочности

A ∪ B = B ∪ A

A ∩ B = B ∩ A

Сочетательное свойство

(A ∪ B) ∪ C = A ∪ (B ∪ C)

(A ∩ B) ∩ C = A ∩ (B ∩ C)

Основные тождества алгебры множеств.

Для произвольных множеств А, В, и С справедливы следующие соотношения (табл. 1):

Таблица 1

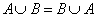
1. Коммутативность объединения	1’. Коммутативность пересечения
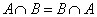
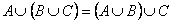
2. Ассоциативность объединения	2’. Ассоциативность пересечения
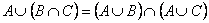
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
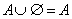
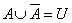
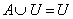
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
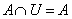
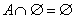
5. Закон идемпотентности объединения	5’. Закон идемпотентности пересечения
6. Закон де Моргана	6’. Закон де Моргана
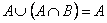
7. Закон поглощения	7’. Закон поглощения
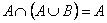
8. Закон склеивания	8’. Закон склеивания
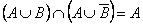
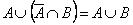
9. Закон Порецкого	9’. Закон Порецкого
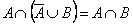
10. Закон двойного дополнения

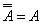
Поиск по сайту: