АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Булевы функции. Способы задания. Примеры

Читайте также:
  1. I. Открытые способы определения поставщика.
  2. I. Ситуационные задачи и тестовые задания.
  3. III. Способы очистки.
  4. MathCad: способы решения системы уравнений.
  5. Ms Excel: мастер функций. Логические функции.
  6. Ms Excel: типы и способы адресации ячеек.
  7. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  8. Абстрактные классы и чистые виртуальные функции. Виртуальные деструкторы. Дружественные функции. Дружественные классы.
  9. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  10. Алгебраическое интерполирование функции.
  11. Асимптоты графика функции.
  12. Б) СПОСОБЫ ПЕРЕВОДА СЛОВ, ОБОЗНАЧАЮЩИХ НАЦИОНАЛЬНО-СПЕЦИФИЧЕСКИЕ РЕАЛИИ

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Пример. Таблица истинности для f1(x1, x2), f2(x1, x2) и f3(x1, x2).

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 22 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n, где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2m=22 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M1f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M1f = {α 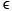B n:f(α) = 1};

M0f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M0f = {α 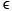B n:f(α) = 0}.

Пример (мажоритарная функция).

M1f = {011,101,110,111}, M0f = {000,001,010,100}. •


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)