АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задание булевой функции вектором ее значений

Читайте также:
  1. II. Основные задачи и функции
  2. III. Предмет, метод и функции философии.
  3. IV. Конструкция бент-функции
  4. Ms Excel: мастер функций. Логические функции.
  5. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  6. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  7. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  8. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  9. V2: Функции исторической науки
  10. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ
  11. Window(x1, y1, x2, y2); Задание окна на экране.
  12. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ

φf=f(0,0, …, 0)f(0,0, …, 1) … f(1,1, …, 1).

Пример (мажоритарная функция).

φf =00010111. •

4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x1, …, xn) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

5) Интервальный способ задания булевой функции. Булеву функцию f(x1, …, xn) можно задать множеством интервалов If = {I1, I2, …, Ik}, объединение которых образует характеристическое множество M1f, то есть I1 I2 … Ik = M1f. Множество интервалов If называется достаточным для функции f(x1, …, xn).

Пример. Мажоритарная функция может быть задана достаточным множеством If = {I1, I2, I3} интервалов:

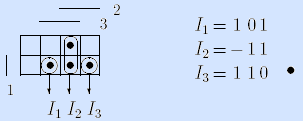
Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

Пример. Зададим мажоритарную функцию другим достаточным множеством I'f = {I1, I2, I3, I4} интервалов:

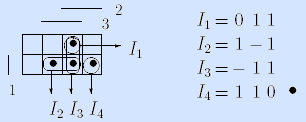
Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I1= – 1 1 – допустимый интервал для мажоритарной функции, I2= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x1, …, xn), если он является допустимым для этой функции, и не существует другого допустимого интервала I', такого что I I'.

Пример. I1= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I2 = 111 не является максимальным, так как I2 I1.

Пример. Зададим мажоритарную функцию множеством I''f = {I1 I2, I3} всех максимальных интервалов.

Определение. Точку булевой функции f(x1, …, xn) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)