Бинарные отношения

Пусть 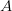и 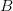два конечных множества. Декартовым произведением множеств 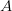и 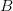называют множество 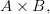состоящее из всех упорядоченных пар, где

Бинарным отношением между элементами множества 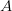и 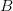называется любое подмножество 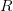множества 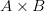, то есть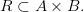

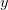По определению, бинарным отношением называется множество пар. Если R — бинарное отношение (т.е. множество пар), то говорят, что параметры и связаны бинарным отношением 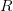, если пара 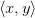является элементом R, т.е.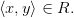

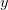Высказывание: «предметы и связаны бинарным отношением 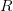» записывают в виде 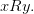Таким образом,

Если 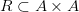, то говорят, что бинарное отношение определено на множестве .

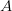Примеры бинарных отношений:

• на множестве целых чисел 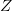отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;
• на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;
• на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

Областью определения бинарного отношения 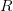называется множество, состоящее из таких , для которых хотя бы для одного .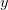
Область определения бинарного отношения будем обозначать .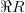

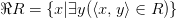
Областью значений бинарного отношения 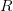называется множество, состоящее из таких 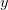, для которых хотя бы для одного .
Область значений бинарного отношения будем обозначать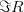

Инверсия (обратное отношение) 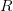— это множество 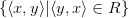и обозначается, как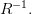

Композиция (суперпозиция) бинарных отношени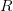й и — это множество и обозначается, как .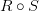

Поиск по сайту: