АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Или метод секущих предполагает более быстрое нахождение корня, чем метод половинного деления

Читайте также:
  1. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  2. B) наиболее часто встречающееся значение признака в данном ряду
  3. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  4. I. Методические основы
  5. I. Предмет и метод теоретической экономики
  6. II. Метод упреждающего вписывания
  7. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  8. II. Методы непрямого остеосинтеза.
  9. II. Проблема источника и метода познания.
  10. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  11. III. Методологические основы истории
  12. III. Предмет, метод и функции философии.

Найдем корень на неизвестном интервале [a;b]. Пусть для определенности , 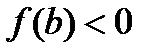. Геометрически данный метод заключается в том, что в качестве приближений принимаются значения точек пересечения хорды с осью абсцисс.

Уравнение хорды, проходящей через точки , :

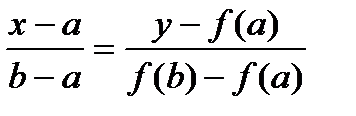
Отсюда, пологая x=x(1) y=0 получим

- это основное уравнение метода хорд.

Далее, сравнивая знаки величин f(a), f(x(1)), f(b) находим, что корень находится в интервале (x(1),b), так как . На следующем шаге определим новое приближение x(2) как точки пересечения хорды A1B и оси абсцисс.

Для 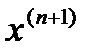и неподвижного конца b имеем:

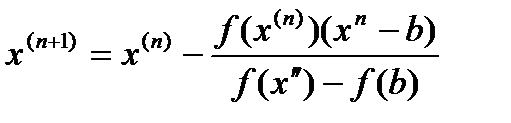
Процесс продолжается до тех пор, пока значение 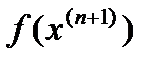не станет по модулю меньше заданной точности. Для оценки абсолютной погрешности можно воспользоваться формулой

Где - наименьшее значение производной на рассматриваемом отрезке. Метод хорд, как частный случай метода деления отрезка, содержащего корень на части, также применим для любых уравнений, и сходится всегда.

 

 

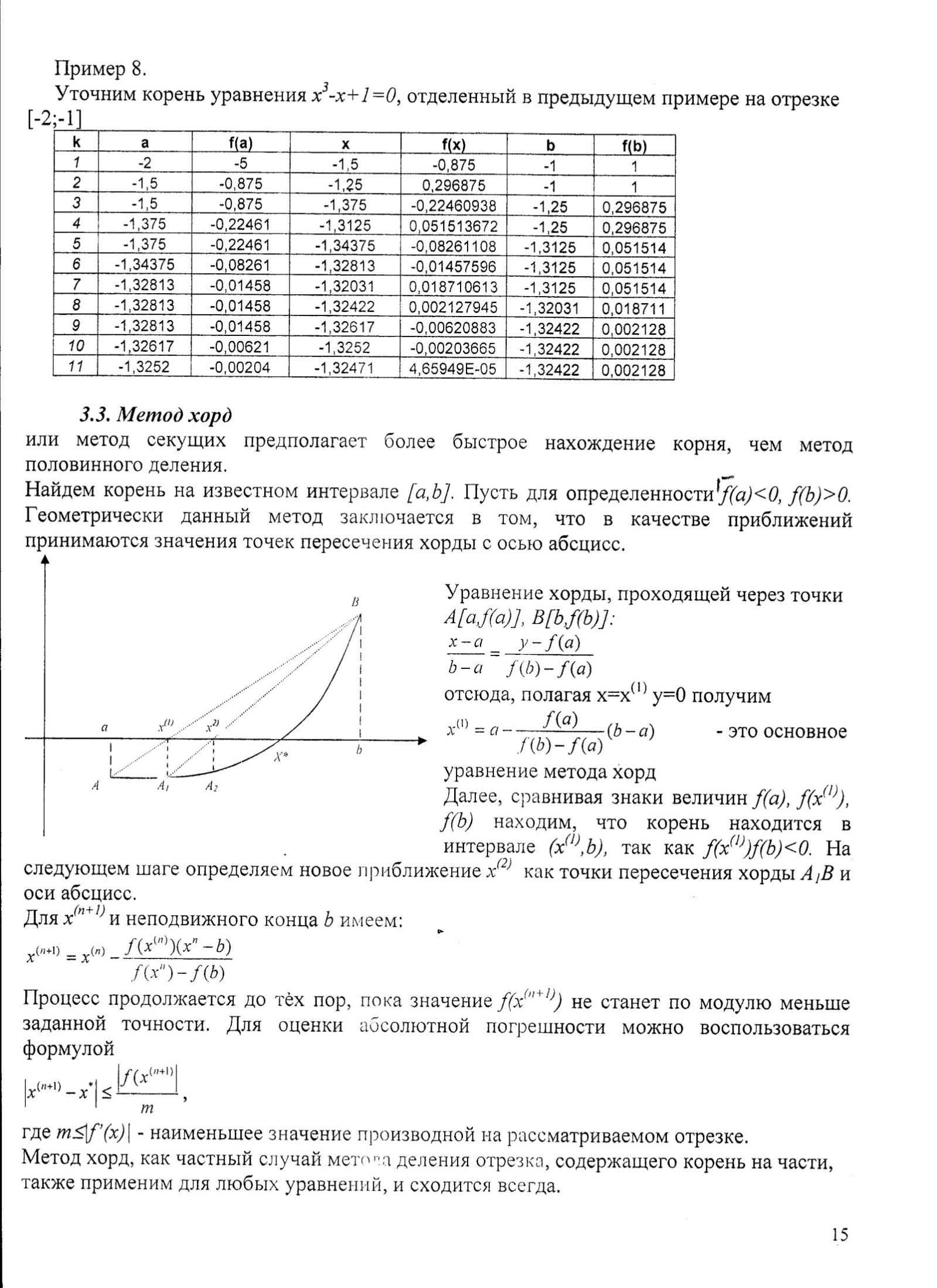
Пример 9.

Уточним корень уравнения 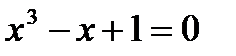на отрезке [-2;-1] методом хорд

k a f(a) x f(x) b f(b)
  -2 -5 -1,16667 0,578703704 -1  
  -2 -5 -1,25311 0,28536303 -1,16667 0,578704
  -2 -5 -1,29344 0,129542093 -1,25311 0,285363
  -2 -5 -1,31128 0,056588487 -1,29344 0,129542
  -2 -5 -1,31899 0,024303747 -1,31128 0,056588
  -2 -5 -1,32228 0,01036185 -1,31899 0,024304
  -2 -5 -1,32368 0,00440395 -1,32228 0,010362
  -2 -5 -1,32428 0,001869258 -1,32368 0,004404
  -2 -5 -1,32453 0,000792959 -1,32428 0,001869
  -2 -5 -1,32464 0,000336301 -1,32453 0,000793

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)