 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы простых итераций
При большом числе неизвестных схемы прямых методов, дающее точное решение становятся достаточно сложными и удобнее пользоваться приближенными методами решения. Итерационные методы позволяют получать решение с заранее заданной точностью, если доказана сходимость метода. Рассмотрим метод простых итераций.
Дана линейная система:


.................. (1)

Введем рассмотренные матрицы:


 (2)
(2)
Тогда уравнение можно записать в матричном виде:
Ax=b (3)
Предполагая, что диагональные коэффициенты  (i=1,2,…,n) разрешим первое уравнение относительно x1 второе – относительно x2 и т.д., получим эквивалентную систему:
(i=1,2,…,n) разрешим первое уравнение относительно x1 второе – относительно x2 и т.д., получим эквивалентную систему:
 (4)
(4)
Где 
 при i ≠ j и aij = 0 при i = j
при i ≠ j и aij = 0 при i = j
Введем матрицы 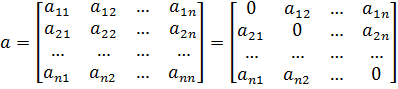
и 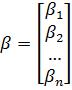 , тогда систему (4) можно записать в матричном виде:
, тогда систему (4) можно записать в матричном виде:
 (5)
(5)
Будем решать систему методом последовательных приближений. За нулевое приближение принимаем столбец свободных членов x(0)=β, далее последовательно строим матрицы-столбцы в первом приближении:
 , далее во втором приближении:
, далее во втором приближении:
 и т.д.
и т.д.
Общая формула вычисления приближений:
 или
или 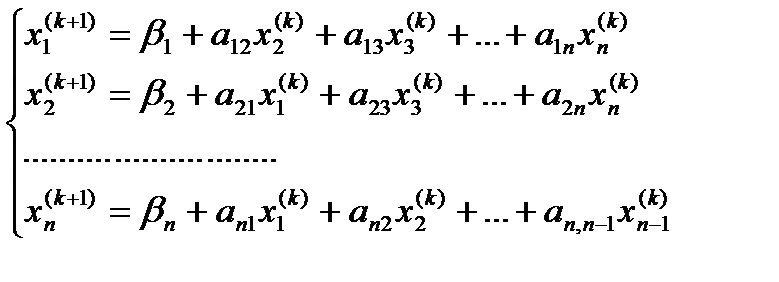 (6)
(6)
Если последовательность приближений x(0), x(1),…, x(k) имеет предел
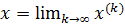 , то этот предел является решением системы (4).
, то этот предел является решением системы (4).
Приведем без доказательства достаточное условие сходимости итераций.
Теорема.
Если для приведенной системы (4) выполнено, по крайней мере, одно из условий:
1)  (i=1,2,…,n)
(i=1,2,…,n)
2)  (j=1,2,…,n)
(j=1,2,…,n)
То процесс итерации сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие.
Для исходной системы (2) 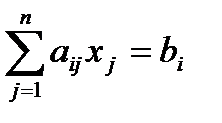 (i=1,2,…,n) метод итерации сходится, если выполнены неравенства:
(i=1,2,…,n) метод итерации сходится, если выполнены неравенства:  (i=1,2,…,n), т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
(i=1,2,…,n), т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Процесс итерации хорошо сходится, если элементы матрицы a малы по абсолютной величине. Иными словами, модули диагональных элементов системы (2) должны быть велики по сравнению с модулями недиагональных коэффициентов (свободные члены при этом роли не играют).
Пример 5.
Методом простых итераций решим систему:
Шаг 1. Приведем систему к виду, удобному для итерации:
| X1 | X2 | X3 | ||
| x1 | 1,2 | -0,1 | -0,1 | |
| x2 | 1,3 | -0,2 | -0,1 | |
| x3 | 1,4 | -0,2 | -0,2 |
Начальные приближения:
| k | x1 | x2 | x3 |
| 1,2 | 1,3 | 1,4 | |
| 0,93 | 0,92 | 0,9 | |
| 1,018 | 1,024 | 1,03 | |
| 0,9946 | 0,9934 | 0,9916 | |
| 1,0015 | 1,00192 | 1,0024 | |
| 0,999568 | 0,99946 | 0,999316 | |
| 1,000122 | 1,000155 | 1,000194 | |
| 0,999965 | 0,999956 | 0,999945 | |
| 1,00001 | 1,000013 | 1,000016 | |
| 0,999997 | 0,999996 | 0,999996 | |
| 1,000001 | 1,000001 | 1,000001 |
Поиск по сайту: