АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Или метод дихотомии основан на делении отрезка, содержащего корень пополам

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

Пусть действительный корень уравнения f(x)=0 отделен и функция непрерывна на интервале [a,b] отделения корня. Построим процесс сужения интервала [a,b] так, чтобы искомый корень всегда находился внутри суженного интервала. Очевидно, в этом случае погрешность приближенного значения корня не превышает 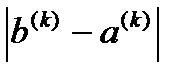, где b(k), a(k) – граничные точки интервала на k-ой итерации.

Найдем середину отрезка и примем ее за

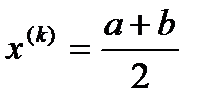(3.2)

Если 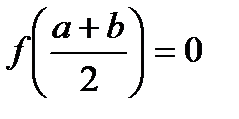, то x(k) и есть корень уравнения, если f(x)≠0, вычислим произведения 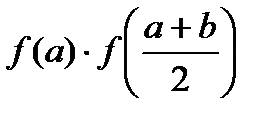и 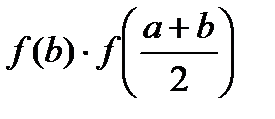, из двух половин отрезка выберем тот, в котором произведение является отрицательной величиной и обозначаем новые границы отрезка через a(1)b(1) и т.д.

Погрешность метода половинного деления или метода дихотомии определяется соотношением: 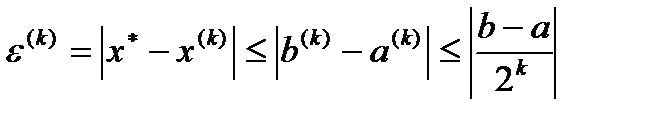, которое указывает на скорость сходимости метода: с увеличением k погрешность стремится к нулю как геометрическая прогрессия со значением q=1/2.

Метод половинного деления применим для любых уравнений, и сходится всегда.

 

Пример 8.

Уточним корень уравнения 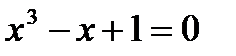, отделенный в предыдущем примере на отрезке [-2;-1]

k a f(a) x f(x) b f(b)
  -2 -5 -1,5 -0,875 -1  
  -1,5 -0,875 -1,25 0,296875 -1  
  -1,5 -0,875 -1,375 -0,22460938 -1,25 0,296875
  -1,375 -0,22461 -1,3125 0,051513672 -1,25 0,296875
  -1,375 -0,22461 -1,34375 -0,08261108 -1,3125 0,051514
  -1,34375 -0,08261 -1,32813 -0,01457596 -1,3125 0,051514
  -1,32813 -0,01458 -1,32031 0,018710613 -1,3125 0,051514
  -1,32813 -0,01458 -1,32422 0,002127945 -1,32031 0,018711
  -1,32813 -0,01458 -1,32617 -0,00620883 -1,32422 0,002128
  -1,32617 -0,00621 -1,3252 -0,00203665 -1,32422 0,002128
  -1,3252 -0,00204 -1,32471 4,65949E-05 -1,32422 0,002128

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)