 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод простой итерации. Для использования этого метода нелинейное уравнение нужно записать в виде (1)
Для использования этого метода нелинейное уравнение  нужно записать в виде (1)
нужно записать в виде (1)
Тогда по известному начальному приближению строятся итерации для получения новых, более точных приближений по формуле:
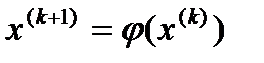 (2)
(2)
Итерационный процесс прекращается после достижения заданной точности
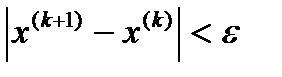 (3)
(3)
Исследуем процесс сходимости метода. Если  имеет непрерывную производную, то из теоремы Лагранжа о конечном приращении
имеет непрерывную производную, то из теоремы Лагранжа о конечном приращении
 (4)
(4)
Следует, что точка  лежит между точками
лежит между точками  и
и  . Поэтому если всюду
. Поэтому если всюду  на всем отрезке [a,b]. Если
на всем отрезке [a,b]. Если  , то итерации могут не сходиться. Если
, то итерации могут не сходиться. Если  , но вдали от корня
, но вдали от корня  , то итерации сходятся, если начальное приближение выбрано достаточно близко к корню. При произвольном начальном приближении сходимости может не быть. Чтобы обеспечить сходимость необходимо подобрать функции
, то итерации сходятся, если начальное приближение выбрано достаточно близко к корню. При произвольном начальном приближении сходимости может не быть. Чтобы обеспечить сходимость необходимо подобрать функции  соответствующим образом.
соответствующим образом.
Пример 11.
Уравнение 
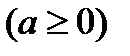 преобразуем к виду (1) тремя способами:
преобразуем к виду (1) тремя способами:

| 
| Поведение 
| Сходимость метода |

| 
|  при при 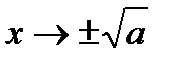
| Не сходится |

| 
|  при при 
 при при 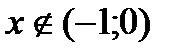
| Сходится в ограниченном интервале к отрицательному значению корня |

| 
|  при при 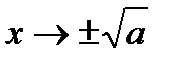
| Сходится и очень быстро |
Пример 12.
Уточним корень уравнения  на отрезке [-2;-1] методом простой итерации. Необходимо представить функцию в виде приведенной функции для проведения итерационного процесса и проверим условие сходимости.
на отрезке [-2;-1] методом простой итерации. Необходимо представить функцию в виде приведенной функции для проведения итерационного процесса и проверим условие сходимости.
1. Представим функцию в следующем виде:

 ;
;  при
при 
 , т.е. сходимость будет в ограниченном интервале и если корень находится именно на этом же интервале, проверим:
, т.е. сходимость будет в ограниченном интервале и если корень находится именно на этом же интервале, проверим:
| k | x | f(x) |
| -1 | ||
| 3,89E+08 |
Из таблицы видно, что решение будет расходиться с увеличением шага, даже если взять начальное приближение из интервала сходимости.
2. Необходимо представить функцию в таком виде, чтобы выполнилось условие сходимости:

 ;
; 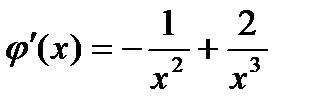

 , т.е.на всем протяжении кроме ограниченного интервала, именно в этом интервале лежит корень уравнения.
, т.е.на всем протяжении кроме ограниченного интервала, именно в этом интервале лежит корень уравнения.
| k | x | f(x) |
| -1 | ||
| -2 | -5 | |
| -0,75 | 1,328125 | |
| -3,11111 | -26,0014 | |
| -0,42474 | 1,348117 | |
| -7,89734 | -483,644 |
3. 


 , на всем протяжении, кроме ограниченного интервала, т.к. корень находится за пределами этого интервала, то решение может получиться. Проверим: шаге до 3 знака.
, на всем протяжении, кроме ограниченного интервала, т.к. корень находится за пределами этого интервала, то решение может получиться. Проверим: шаге до 3 знака.
| k | x | f(x) |
| -1,5 | -0,875 | |
| -1,24074 | 0,330698 | |
| -1,41388 | -0,41253 | |
| -1,26792 | 0,229581 | |
| -1,38055 | -0,25068 | |
| -1,28528 | 0,162059 | |
| -1,36161 | -0,16279 | |
| -1,29712 | 0,114674 | |
| -1,34967 | -0,10889 |
Поиск по сайту: