Методы отделения корней

Под отделение корня понимается определение промежутка, содержащего единственный корень уравнения. Одна из точек этого промежутка принимается за начальное приближение корня. В зависимости от метода, который предполагается использовать для уточнении корня, требуется определение тех или иных свойств отдельного корня и поведения функции на отрезке отделения. В общем случае этап отделения корня не может быть алгоритмизирован. Для некоторых классов уравнений разработаны специальные приемы.

Для отделения действительных корней полезно определять заранее число корней, а также верхнюю и нижнюю границы их расположения. Для этого используется ряд теорем.

Теорема 1. (о числе корней алгебраического уравнения)

Алгебраическое уравнение n-ой степени вида: ,

где a_n,…, a₀ – коэффициенты уравнения – действительные числа, имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

Теорема 2. (о парной сопряженности комплексных корней)

Если - корень алгебраического уравнения кратности k, то число также является корнем той же кратности.

Следствие.

Алгебраическое уравнение нечетной степени имеет по крайней мере один действительный корень.

Теорема 3. (об оценке модулей корней уравнения)

Пусть , (максимальные из соответствующих коэффициентов уравнения), тогда модули всех корней (i=1,…,n) уравнения удовлетворяют неравенству: , i=1,…,n, т.е. корни уравнения расположены в кольце.

Следствие.

Числа , являются соответственно нижней и верхней границей положительных корней уравнения: . Аналогично нижняя и верхняя граница отрицательных корней определяется как

Теорема 4. (Декарта о количестве действительных корней алгебраических уравнений)

Число S₁ положительных корней (с учетом их кратностей) алгебраического уравнения равно числу перемен знаков в последовательности коэффициентов

a_n, a_n-1,…,a₀ многочлена (коэффициенты равные нулю не учитываются) или меньше этого числа на четное число. Число S₂ отрицательных корней (с учетом их кратностей) алгебраического уравнения равно числу перемен знаков в последовательности коэффициентов a_n, a_n-1,…,a₀ многочлена

Теорема 5.

1. Если функция f(x) на концах отрезка [a,b] принимает значения разных знаков, т.е. f(a)f(b)<0, то на этом отрезке содержится по крайней мере один корень уравнения.

2. Если же функция f(x) непрерывна и дифференцируема и ее производная сохраняет знак внутри отрезка [a,b], то на этом отрезке находится единственный корень уравнения.

В вычислительной практике обычно используют следующие способы отделения корней:

1. Построение графиков функции.

2. Формирование простых функций, таких, что получается равносильное уравнение (имеющее одинаковые корни): , где функции f₁(x), f₂(x) – более простые, чем исходная функция f(x). Тогда нулями функции f(x) будут являться абсциссы точек пересечения функций f₁(x) и f₂(x).

3. Средства мат. анализа, с помощью исследования функций и построения графиков. Например, Если существует непрерывная производная f '(x), и корни уравнения f '(x)=0 легко вычисляются, то достаточно подсчитать знаки функции f(x) в точках нулей производной и в граничных точках.

Пример 7.

Необходимо отделить корни уравнения

1. По теореме 1 – это уравнение имеет три корня, по следствию из теоремы 2 – по крайней мере, один из них действительный.

2. Оценим модули корней уравнения по теореме 3:Так как , , то или

отсюда и

3. Определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена P₃(x): 1, 0, -1, 1. Так как число перемен знака S₁=2 (нулевой коэффициент не учитывается), то число положительных корней =2 или меньше на четное число, т.е. их нет. Далее выписываем коэффициенты многочлена P₃(-x)=-x³+x+1: -1,0,1,1. Так как число перемен знака S₂=1, то число отрицательных корней =1.

4. Сформируем две простые функции, преобразуем уравнение к равносильному виду: и найдем точки пересечения графиков 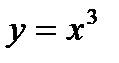и . Из графика видно, что уравнение имеет один действительный корень, который лежит на отрезке [-2;-1].

5. Отделим корни методом математического анализа, для этого найдем производную функции:

Производная , найдем корни производной: , теперь нужно подсчитать знаки функции в граничных точках и точках нулей производной:

X
-∞	-
	+
	+
+∞	+

Следовательно уравнение имеет только 1 действительный корень на промежутке (-∞; ), если учесть проделанные ранее вычисления о границах отрицательных корней, можно сделать вывод, что корень находится в промежутке -2<x< ,, либо, не используя предыдущие вычисления, можно поделить интервал на более мелкие и проверить знаки функции на границах, т.е. вместо точки -∞ нужно подставить реальное число, например -10, отрезок (-10; ), далее можно поделить и этот отрезок пополам: (5; ), и т.д.

Поиск по сайту: