 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод Ньютона. Пусть x* корень уравнения отделен на отрезке [a,b], причем , непрерывны и сохраняют отдельные знаки при
Пусть x* корень уравнения  отделен на отрезке [a,b], причем
отделен на отрезке [a,b], причем 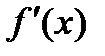 ,
, 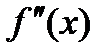 непрерывны и сохраняют отдельные знаки при
непрерывны и сохраняют отдельные знаки при 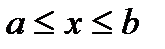 . Пусть найдено приближенное значение корня x(k), а погрешность
. Пусть найдено приближенное значение корня x(k), а погрешность
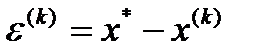 (1)-малая величина
(1)-малая величина
Разложим функцию в точке x* в

Отсюда найдем погрешность:
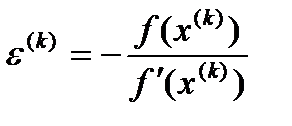 (2)
(2)
Сравним соотношение для погрешности (1) и (2) и выразим x*, учитывая при этом, что мы получим только уточненное приближенное значение корня:
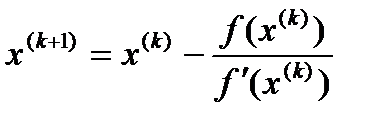 (3) - это основное соотношение метода Ньютона.
(3) - это основное соотношение метода Ньютона.
Геометрически этот процесс означает замену на каждой итерации кривой 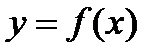 на касательную к ней в некоторой точке и определение значение приближенного значения корня как координаты точки пересечения касательной с осью абсцисс.
на касательную к ней в некоторой точке и определение значение приближенного значения корня как координаты точки пересечения касательной с осью абсцисс.
 В качестве начального приближения удобно выбрать одну из граничных точек отрезка: a или b. Для выбора хорошего приближения x(0) должно выполняться условие
В качестве начального приближения удобно выбрать одну из граничных точек отрезка: a или b. Для выбора хорошего приближения x(0) должно выполняться условие 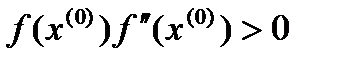 . Выберем начальное приближение x0=b, для которого
. Выберем начальное приближение x0=b, для которого  проведем касательную к кривой в точке
проведем касательную к кривой в точке  , точка пересечения касательной с осью абсцисс будет первым приближение корня x(1).
, точка пересечения касательной с осью абсцисс будет первым приближение корня x(1).
Запишем уравнение касательной в точке 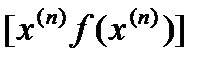 :
:
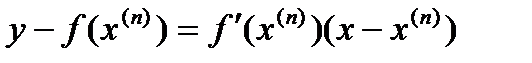
Полагая y=0, x=x(n+1) также можно получить соотношение метода Ньютона (3)
Заметим, что немаловажен выбор хорошего начального приближения: если мы возьмем точку x(0)=a, для которой 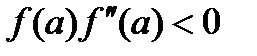 , то пересечение касательной с осью Ох даст нам точку х, лежащую вне отрезка.
, то пересечение касательной с осью Ох даст нам точку х, лежащую вне отрезка.
Оценку погрешности можно провести по формуле из предыдущего параграфа:

Где  - наименьшее значение производной на рассматриваемом отрезке.
- наименьшее значение производной на рассматриваемом отрезке.
Пример 10.
Уточним корень уравнения 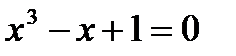 на отрезке [-2, -1] методом Ньютона:
на отрезке [-2, -1] методом Ньютона:
Необходимо правильно выбрать начальное приближение, для этого находим вторую производную:  ;
; 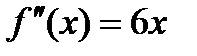 . Проверяем знаки произведения для точки a:
. Проверяем знаки произведения для точки a: 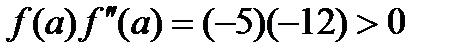 , следовательно в качестве начального приближения выбираем точку a и начинаем итерации по формуле Ньютона:
, следовательно в качестве начального приближения выбираем точку a и начинаем итерации по формуле Ньютона:
| k | x | f(x) | f’(x) |
| -2 | -5 | ||
| -1,54545 | -1,14576 | 6,165289 | |
| -1,35961 | -0,1537 | 4,545658 | |
| -1,3258 | -0,00462 | 4,273248 | |
| -1,32472 | -4,7E-06 | 4,264642 |
Поиск по сайту: