Тема 2. Численные методы решения систем линейных уравнений

Требуется найти решение системы линейных уравнений:

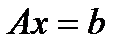
Где 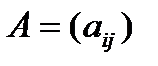квадратная матрица коэффициентов, 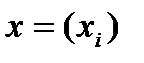вектор-столбец неизвестных, 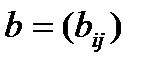– вектор-столбец правых частей системы. По правилу Крамера система имеет единственное верное решение, если определитель не равен нулю det A≠0, система является невырожденной. Если же определитель матрицы равен нулю, то система называется вырожденной и либо не имеет решений (при b≠0), либо имеет бесчисленное множество решений (при b=0). Существуют так же почти невырожденные системы – определитель которых близок к нулю, но отличен от нуля (det A≈0). Небольшие изменения коэффициентов матрицы системы или правых частей системы в таких системах могут привести к большим погрешностям решения.

Можно графически проиллюстрировать все эти 3 случая на примере системы 2-х линейных уравнений:

На рис. 1.1 каждому уровню соответствует прямая на плоскости, точка пересечения этих прямых и есть решение системы.

Если det A=0, то наклоны прямых равны и они либо параллельны, либо совпадают. При det A≈0 небольшие погрешности в коэффициентах и правых частях могут привести к большим погрешностям в решении, т.е. к неточному определению точки пересечения, т.к. при таком расположении прямых она как бы размыта. Системы такого типа называют плохо обусловленными.

Рис. 1.1

Методы решения СЛУ делятся на прямые и итерационные. Прямые методы дают решение задачи за конечное (точно определяемой для каждого метода) число операций. Итерационные методы дают решение как предел бесконечной последовательности приближенных решений, в которых каждое последующее более точное приближение находится по уже найденному предыдущему решению.

Поиск по сайту: