Структура погрешности

Введение.

В настоящее время численные методы являются мощным математическим средством решения многих научно-технических проблем. Это связанно как с невозможностью в большинстве случаев получить точное аналитическое решение, так и со стремительным развитием компьютерной техники. Существуют многочисленные стандартные программы и объективно-ориентированные пакеты прикладных программ. Однако научным и инженерно-техническим работникам важно понимать сущность основных численным методов и алгоритмов, поскольку зачастую интерпретация результатов расчетов нетривиальна и требует социальных знаний особенностей применяемых методов. Поэтому необходимо уделять большое внимание структуре погрешностей при решении конкретных задач и корректности вычислений.

Тема 1. Погрешности. Действия с приближенными числами.

Структура погрешности.

Существует 4 источника погрешностей, полученных в результате численного решения:

- математическая и физическая модели;

- исходные данные;

- приближенность метода;

- ошибки округления.

Первые 2 источника погрешностей проводят к так называемой неустранимой погрешности. Эта погрешность может присутствовать, даже если решение поставленной задачи найдено точно. Погрешность метода возникает из-за того, что точный оператор и исходные данные, в частности в начальные и краевые условия заменяются по определенным правилам приближенным. Так, производные заменяются их разностными аналогами, интегралы – суммами, функции – специальными многочленами; а при решении задач строятся бесконечные итерационные процессы, которые естественным образом прекращаются после конечного числа итераций. Как правило, погрешность метода может быть оценена и поддается контролю.

Погрешность округления возникает в связи с тем, что вычисления производятся с конечным числом значащих цифр. Очевидно, что погрешность, возникающая при округлении, не превышает младшего составляемого разряда.

Пусть a – точное, неизвестное числовое значение некоторой величины, ᾱ - известное приближенное числовое значение этой величины, тогда число называют абсолютной погрешностью числа a. Разность приближенного и точного значения.

Под предельной абсолютной погрешностью ∆_a приближенного числа понимается всякое число, не меньшее абсолютной погрешности этого числа. Таким образом , тогда точное число заключено в границах . В записи приближенного числа, полученного в результате изменений, обычно отмечают его предельную абсолютную погрешность, например если длина отрезка =214см. с точностью до 0,5см., то пишут см. Абсолютной погрешности недостаточно для характеристики точности измерения. Например, если при измерении длин 2-х стержней получили см и см, то, несмотря на совпадение предельных абсолютных погрешностей качество первого измерения выше, чем второго. Поэтому вводится понятие относительной погрешности.

Величину называют относительной погрешностью. Отношение абсолютной погрешности к модулю приближенного числа.

При сложении и вычитании складываются абсолютные погрешности, а при делении и умножении – относительные погрешности. Абсолютная погрешность характеризуется числом верных цифр после запятой, а относительная погрешность – числом верных значащих цифр.

Поскольку на современных компьютерах число записывается, как правило, с 10-12 десятичными знаками, то погрешность δ единичного округленного порядка 10^-10 – 10^-12 обычно пренебрежимо мала по сравнению с неустранимой погрешностью и погрешностью метода.

Пример 1.

Требуется определить какое из равенств точнее: ;

1. Находим значения данных выражений с большим числом десятичных знаков:

;

2. Вычисляем предельные абсолютные погрешности, вычисляя их с избытком:

;

3. Вычисляем предельные относительные погрешности:

;

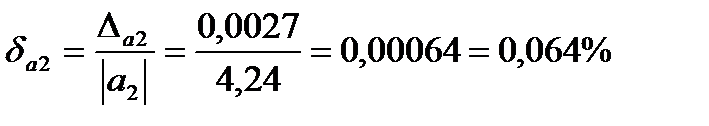
4. Сравнивая предельные относительные погрешности видно, что первое равенство является более точным.

Пример 2.

Необходимо вычислить значение выражения и определить погрешность результата.

; где n=3,0567(±0,0004), m=5,72(±0,02)

1. Найдем предельные абсолютные погрешности выражений в скобках, складывая предельные абсолютные погрешности приближенных чисел:

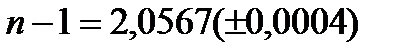
2. Вычислим значения выражения без учета погрешностей:

3. Вычислим значение предельной относительной погрешности выражения путем сложения относительных погрешностей выражений в скобках:

4. Приведем число в нормальной записи приближенного числа с указанием предельной абсолютной погрешности:

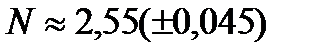
Поиск по сайту: