Метод исключения Гаусса

Рассмотрим систему уравнений:

…………….. или , i=1,…,n (1)

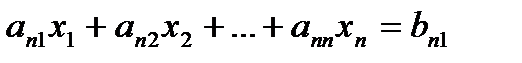
Метод Гауса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее к единичной (обратный ход). Очевидно, если матрица единичная, то

Начнем исследование системы с частного случая, когда матрица системы (1) верхняя треугольная, поэтому при i=j, т.е. когда все элементы ниже главной диагонали равны нулю. Тогда из последнего уравнения сразу определяется x_n:

(2)

Общая формула нахождения остальных x_k:

при k=n-1, n-2,..,1 (3)

Это обратный ход метода Гаусса.

Теперь рассмотрим переведение матрицы системы (1) к верхней треугольной. Вычтем из второго уравнения система (1) первое, умноженное на такое число, при котором коэффициент при x₁ обратится в нуль. То же проделаем со всеми остальными уравнениями. В результате все коэффициенты первого столбца, лежащие ниже главной диагонали, обратятся в нуль. Затем, используя второе уравнение, обратим в нуль соответствующие коэффициенты второго столбца. Последовательно продолжая этот процесс, приведем матрицу системы к верхней треугольной форме.

Запишем общие формулы прямого хода метода Гаусса. Пусть проведено исключение коэффициентов из (k-1)-го столбца. Тогда останутся уравнения с нулевыми элементами ниже главной диагонали.

, k ≤ i ≤ n (4)

Умножим k-ю строку на число

, m > k (5)

и вычтем из m-й строки. Первый нулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам:

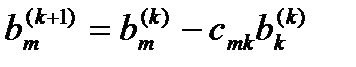, k < m (6)

Проведя вычисления по этим формулам при всех указанных индексах, обратим в нуль элементы k-го столбца, лежащие ниже главной диагонали.

Запишем треугольную систему, получающуюся после выполнения всех вычислений прямого хода. На освободившиеся места в нижней половине матрицы системы поставим множитель c_mk, их нужно запоминать, так как они могут потребоваться при обращении матрицы или уточнения решения. Получим систему:

(7)

Треугольная матрица легко решается обратным ходом.

На некотором шаге прямого хода может оказаться, что коэффициент , но мал по сравнению с остальными элементами матрицы системы, или мал по сравнению с элементами i-го столбца. Деление коэффициентов системы на малую величину может привести к значительным ошибкам округления. Для уменьшения ошибок каждый цикл вычислений начинают с перестановки строк, среди элементов столбца находят наибольший по модулю и перестановкой строк переводят его на главную диагональ. Такая модификация метода называется методом Гаусса с выбором главного элемента. Для контроля расчета полезно найти невязки:

, 1 ≤ k ≤ n (8)

Если они велики, то это означает грубую ошибку в расчетах (ошибка в программе), если малы, а система хорошо обусловлена, то решение найдено достаточно точно, хотя для плохо обусловленной системы малость невязок не гарантирует хорошей точности решения.

Пример 3.

Система уравнений

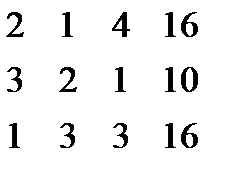
Разделим 1-ую строку на 2 и обнулим элементы ниже 1-го в 1-м столбце

k=2, приводим второй элемент матрицы: делим 2-ю строку на 0,5 и обнулим элемент в 3-ей строке

k=3 разделим элементы третьей строки

Найдем неизвестные из полученной системы:

X3= 3

X2= 2

X3= 1

Проверка правильности решения:

Поиск по сайту: