 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Однородные системы. Условия существования нулевых решений
Рассмотрим АХ=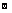 
, = 
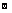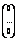, Х= 
- векторстолбец.
Эта однородная система всегда является совместной, т.к. она всегда имеет решение х=0. Решения этой системы обладают свойствами:
Если х1 и х2 являются решениями системы, то 
так же является решением этой системы.
Говорят, что решение однородной системы образует конечномерное линейное векторное пространство.
Пусть имеется 
векторов: 
.
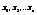Векторы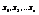 
называют линейно независимыми, если из равенства 
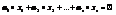следует, что все 
, в противном случае если векторы 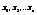линейнозависимые.
Пусть матрица А имеет вид:
, 
, 
, 
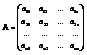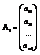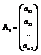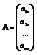
Тогда систему можно записать в виде 
, из равенства видно что если система не имеет не нулевых решений, то векторы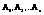 
являются линейнонезависимыми. Если система имеет нулевое решение, то векторы 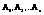являются линейнозависимыми.
Теорема:
Для того чтобы векторы 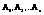были линейнонезависимы, необходимо и достаточно чтобы ранг матрицы А образованный этими элементами равнялся n. Таким образом, чтобы решить однородную систему у-ий АХ= необходимо выполнить следующие действия: вычислить ранг матрицы А, если ранг совпадает с числом неизвестных, то однородная система линейных у-ий имеет одно решение. Если ранг матрицы А меньше числа неизвестных, то в матрице А можно найти S строк и S столбцов, таких, что определитель составленный из элементов лежащих на пересечении выбранных строк и столбцов не равнялся нулю.
Предположим для определённости, что определитель состоит из S строк и S столбцов отличных от нуля, тогда перенося слагаемые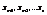 
в правую часть и оставляя в системе первые S уравнений, получим систему:
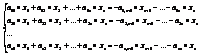(3)
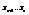- свободные неизвестные (базисные неизвестные), придавая базисным неизвестным произвольные числовые значения из системы (3) можно найти 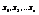, таким образом однородная система линейных у-ий может иметь одно или бесконечное множество решений, отсюда следует, что 
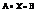может иметь бесконечное кол-во решений или быть несовместной.
Минором k-го порядка называют определитель размерностью (k´k), выбранный из матрицы размерностью (m´n).
Если в матрице А вычёркивается строка Ni, а столбец Nj, то минор, получающийся при удалении строки и столбца называется алгебраическим дополнением.
Наивысший порядок не вырожденных миноров называют – рангом (rang(A))
Поиск по сайту: