Производные и дифференциалы высших порядков. Примеры

Производные высших порядков Рассмотрим функцию y=f(x), определенную на некотором промежутке (a,b). Вычислим производную y', которая также является функцией на (a,b). Производной второго порядка от функции y=f(x) называется производная от ее производной:y''=(y')'. Аналогично определяют производную любого порядка: y⁽ⁿ⁾=(y^(n-1))'.

Дифференциалы высших порядков: Рассмотрим дифференциал функции y=f(x) в произвольной точке промежутка (a,b): dy=f'(x)dx. Здесь dx - приращение независимой переменной, которое является числом и не зависит от x. Сам же дифференциал есть функция от x, и можно вычислить дифференциал от этой функции: d(dy)=(f'(x)dx)'dx₁ При dx=dx₁ этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле d²y=f''(x)dx² Аналогично вычисляется дифференциал любого порядка dⁿy=f⁽ⁿ⁾(x)dxⁿ.

Производные n -го порядка от основных элементарных функций

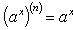
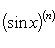
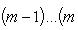
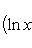
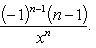
43. Необходимое условие экстремума дифференцируемой. Теорема Ферма. функции в точке x₀ функция достигает экстремума, если для любых x из некоторой окрестности точки x₀ выполняется неравенство f (x) ≤ f (x₀) (минимум) или f (x) ≥ f (x₀) (максимум). Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю. Теорема Ферма. Если функция f (x) дифференцируема в точке x₀ и достигает в ней экстремума, то

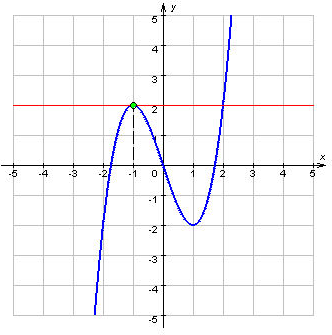
График.Теорема Ферма: касательная к графику функции в точке экстремума параллельна оси абсцисс

Поиск по сайту: