АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение кривых в полярных координатах

Читайте также:
  1. V2: Волны. Уравнение волны
  2. V2: Уравнение Шредингера
  3. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  5. Алгоритм цифровой подписи на основе эллиптических кривых ECDSA
  6. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  7. В простом случае обычное дифференциальное уравнение имеет вид
  8. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  9. Волна вероятности. Уравнение Шредингера
  10. Волновая функция.Уравнение Шредингера
  11. Волновое уравнение для упругих волн и его общее решение.
  12. Волновое уравнение для электромагнитных волн

Окружность

Круг, заданный уравнением .

Общее уравнение окружности с центром в () и радиусом имеет вид:

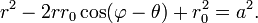
Это уравнение может быть упрощено для частных случаев, например

является уравнением, определяющим окружность с центром в полюсе и радиусом .[15]

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

где — угол, на который прямая отклоняется от полярной оси, то есть, где 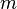— наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)