Конические сечения

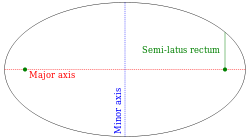
Эллипс.

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

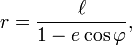
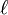где — эксцентриситет, а — фокальный параметр. Если , это уравнение определяет гиперболу; если 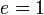, то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .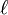

17. Прямая на плоскости. Различные виды уравнения прямой. Расстояние от точки до прямой.
Рассмотрим прямую проходящую через точки М1М2, пусть М произвольная точка лежащая на этой прямой тогда векторы ММ2 и М1М являются коллинеарными. Вектор ММ2 = (X2 – X; Y2 – Y), M1M = (X - X1; Y – Y1). Из условия коллинеарности векторов, следует, что 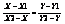1). 1) -уравнение прямой, проходящей через две заданные точки пусть X2 – X1 = K, Y2 – Y1 = L, тогда вектор a = (K; L) параллельна данной прямой направляющий вектор 1) может быть записано в виде: 2). 2) -уравнением прямой проходящей через данную точку М1 в заданном направлении 2) каноническим уравнением прямой. Если три точки М1, М2 и М лежат на одной прямой, то площадь треугольника равна нулю. 3). 3) – уравнение прямой в виде определителя приравняем отношение равенства 1) к некоторому числу T. X - X1 = (X2 – X) T, X –X1 = KT; Y – Y1 = (Y2 –Y1) T, Y – Y1 = LT. (X = X1 + KT, Y = Y1 + LT 4)). 4) – называется параметрическим уравнением. Пусть на плоскости заданы две точки A и B, лежащие на координатных осях A(a; 0), B(b; 0). Найдем уравнение прямой проходящей через точки A и B. 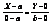; ; 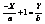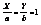- 5). 5) – называется уравнением прямой на отрезке.

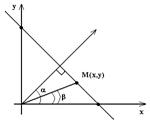
Нормальное уравнение прямой. Пусть прямаяпроходит через точку М(X; Y) перпендикулярно отрезку OP. Длина отрезка 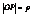, , 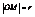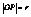cos , p = r(cosacos + sinasinb), p = (r cosb)cosa + (r sinb)sina. X cosa + Y sinb = p – нормальное уравнение прямой.

Расстояние от точки до прямой.
Пусть дана какая – нибудь прямая и произвольная точка М*; обозначим через d расстояние точки М* от данной прямой. Отклонением d точки М* от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и –d, если данная точка и начало координат расположены по одну сторону от данной прямой. Если даны координаты X*, Y* точки М* и нормальное уравнение прямой X cosa + Y sina - p = 0, то отклонение d точки М* от этой прямой может быть вычислено по формуле d = X* cosa + Y* sina - p. Таким образом, чтобы найти отклонение какой – нибудь точки М* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки М*. Полученное число будет равно искомому отклонению. Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: d = 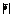. Если дано общее уравнение прямой Ax + By + C = 0, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель m, определяемый формулой 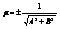. Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

18. Взаимное расположение прямых на плоскости.
Пусть на плоскости заданы две прямые:A1x + B1y +C1 = 0 A2x + B2y + C2 = 0 – 1). Возможны следующие случаи взаимного расположения этих прямых: 1) Прямые пересекаются в одной единственной точке, это означает, что система 1) имеет единственное решение. 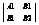¹ 0. 2) Прямые параллельны и не совпадают, это означает, что система 1) не имеет решений. В соответствии с теоремой Капели – это возможно тогда и только тогда, когда rang не совпадает с rang 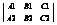. 3) прямые совпадают, это означает, что система 1) имеет множество решений. Это возможно тогда, когда rang совпадает с rang 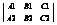. Это возможно в том случае, когда коэффициенты пропорциональны: .

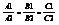Поиск по сайту: