АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение линии пересечения двух поверхностей с помощью концентрических сфер

Читайте также:
  1. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  2. I. Расчет производительности технологической линии
  3. III. Определение оптимального уровня денежных средств.
  4. III. Решение логических задач с помощью рассуждений
  5. V. Множественные волнообразные линии
  6. Автоматизированное рабочее место (АРМ) специалиста. Повышение эффективности деятельности специалистов с помощью АРМов
  7. Аксиомы науки о безопасности жизнедеятельности. Определение и сущность.
  8. Активация поверхностей диэлектриков
  9. Анализ и синтез систем управления с помощью математических теорий
  10. Анализ функциональной связи между затратами, объемом продаж и прибылью. Определение безубыточного объема продаж и зоны безопасности предприятия
  11. Аппаратура линии связи: аппаратура передачи данных, оконечное оборудование, промежуточная аппаратура.
  12. АРГОНАВТЫ ОБРАЩАЮТСЯ ЗА ПОМОЩЬЮ К МЕДЕЕ

Данный способ применяется, если способ секущих плоскостей дает сложные кривые (при пересечении двух конусов вращения плоскостями будем получать окружности и гиперболы) и оси поверхностей пересекаются и лежат в плоскости уровня.

Пример: Определить линию пересечения двух конических поверхностей представленных на рис. 13 и на комплексном чертеже (рис. 14).

 

 

Рис. 13

 

Рис. 14

Построение начнем с определения опорных точек.

В качестве первой поверхности посредника выберем главную меридианальную плоскость Г0 (Г01), которая будет пересекать поверхности конусов по главным меридианам (фронтальные очерки поверхностей рис. 15).

Рис. 14

На фронтальной пл. проекций найдем точки пересечения главных меридиан – А(А2) и В(В2) (рис. 15).Горизонтальныепроекции этих точек А1 и В1 найдем по линиям связи, учитывая, что они принадлежат как поверхностям конусов, так и плоскости Г0(Г01). Точки А и В являются соответственно высшей и низшей точкой линии пересечения.

Рис. 15

Далее определяем границы видимости.

Так как плоскость Г0 является плоскостью симметрии, то она будет делить поверхности и линию пересечения на две симметричные части. Одну часть линии мы будем видеть на фронтальной плоскости проекции, а другую не будем видеть, поэтому границей видимости будут точки А(А2) и В(В2).

На горизонтальной плоскости проекции, линию пересечения по отношении к поверхности конуса, мы будем видеть полностью, а по отношению к поверхности усеченного конуса граница видимости будет проходить через главный меридиан.

В качестве второй поверхности посредника выберем плоскость, проходящую через главный меридиан поверхности усеченного конуса- Г (Г2).

Линия пересечения с поверхностью конусапараллель, а с усечённым конусом – главный меридиан (рис.16).

Рис. 16

 

На горизонтальной плоскости проекции определяем точки пересечения 11 и 1´1 этих линий. Проецируем точки 11 и 1´1 на фронтальную плоскость, учитывая, что они принадлежат как поверхностям конусов, так и плоскости Г1(Г12) (рис. 17).

Рис. 17

 

В заключении определяем промежуточные точки. Находим их с помощью вспомогательных сфер, центр которых лежит в точке пересечения осей поверхностей О. Радиусы сфер определяют в промежутке Rmin - Rmax.

Rmin – радиус вписанной сферы в одну из поверхностей и пересекающей другую поверхность.

Rmax – определяют, как расстояние от центра сферы до наиболее удаленной точки линии пересечения (в данном случае точка В).

Вписываем сферу в конус (рис. 18).

Рис 18

На комплексном чертеже Rmin определяем как перпендикуляр опущенный из точки О (О2) на образующую поверхности конуса. Строим очерк сферы. Рассмотрим сферу, как поверхность соосную с конусом. Сфера будет касаться конуса по окружности, которая на фронтальную плоскость спроецируется в отрезок прямой, так как окружность лежит в плоскости параллельной горизонтальной плоскости проекций. На горизонтальную плоскость проекций эта окружность спроецируется в истинную величину. Теперь рассмотрим сферу, как поверхность соосную с усеченным конусом. Сфера будет пересекать поверхность по окружности, лежащей в плоскости параллельной профильной плоскости проекций. На фронтальную плоскость эта окружность спроецируется в отрезок прямой. Точки 2 (22), и 2'(2'2), - точки пересечения двух полученных построением окружностей. Горизонтальные проекции этих точек находим, использую параллель конуса (рис. 19)

Рис. 20

 

Далее выбираем сферу радиусом Rmin > R < Rmax (рис. 21), которая будет пересекать поверхности двух конусов.

Рис. 21.

На рис. 22 показано как происходит пересечение сферы с коническими поверхностями.

Рис. 22

На фронтальной плоскости проекций строим очерк сферы, аналогично предыдущему определяем линии пересечения сферы с поверхностями конусов,а затем точки пересеченияданных окружностей 3 и 3 ´ (рис.23).

Рис. 23

В заключении соединяем найденные точки и получаем на комплексном чертеже линию пересечения (рис. 24).

 

Рис. 24

. На рис. 25 показан вид этих поверхностей спереди (фронтальная проекция) и сверху (горизонтальная проекция)

 

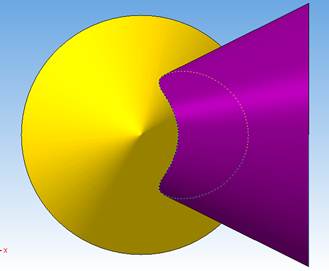
Рис. 25


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)