АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Способ вспомогательных сфер

Читайте также:
  1. I. Открытые способы определения поставщика.
  2. II. Решение логических задач табличным способом
  3. III. Глава о необычных способностях.
  4. III. Способы очистки.
  5. Абиотические факторы и приспособления к ним
  6. Абстрактное мышление – высокая способность к обучаемости.
  7. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  8. Анализ и оценка реальных возможностей восстановления платежеспособности предприятия
  9. Анализ как способ развития экономического мышления
  10. Анализ конкурентоспособности продукции
  11. АНАЛИЗ КРЕДИТОСПОСОБНОСТИ КРЕДИТОПОЛУЧАТЕЛЯ
  12. Анализ ликвидности и платежеспособности

Если использование плоскостей в качестве поверхностей посредников не дает рационального решения, то в качестве поверхностей посредников могут быть использованы сферы. Существует теорема, согласно которой:

Две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридиан поверхностей.

Плоскости сечений (окружностей) перпендикулярны оси вращения, а центры окружностей лежат на оси (рис. 12).

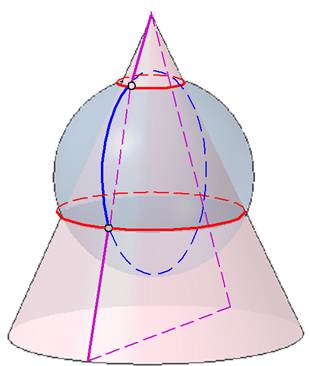
Рис. 12

 

Сфера имеет бесчисленное множество осей вращения, поэтому она может быть соосной одновременно с несколькими поверхностями. Это свойство сферы и используется для построения линии пересечения поверхностей.

С помощью сферических поверхностей легко решаются задачи по определению линии пересечения двух поверхностей вращения, имеющих общую плоскость симметрии, при этом возможны два случая:

v Если оси симметрии пересекаются, то для определения линии пересечения поверхностей используют ряд концентрических сфер.

v Если оси не пересекаются, применяют семейство эксцентрических сфер


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)