 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Бесконечно - малые последовательности
Определение 1. Последовательность  называется бесконечно-малой последовательностью, если
называется бесконечно-малой последовательностью, если  , т.е. если
, т.е. если
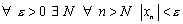 .
.
Определение 2. Последовательность  называется бесконечно-большой последовательностью, если
называется бесконечно-большой последовательностью, если  (это записывается еще и так:
(это записывается еще и так:  , не учитывая знака перед
, не учитывая знака перед 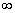 ), т.е. если
), т.е. если
 .Изучим некоторые свойства этих последовательностей.
.Изучим некоторые свойства этих последовательностей.
10. Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.
Доказательство:
 - б.м.п. =>
- б.м.п. =>

 - б.м.п. =>
- б.м.п. =>
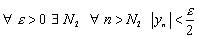
Возьмем  . Тогда
. Тогда

откуда следует, что 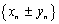 есть б.м.п.
есть б.м.п.
Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п
20. Произведение б.м.п на ограниченную последовательность есть б.м.п.
Доказательство:
 - ограничена. =>
- ограничена. =>

 - б.м.п. =>
- б.м.п. =>
 .
.
Но тогда 
отсюда и следует, что  есть б.м.п.
есть б.м.п.
3. Б.м.п. ограничена
Доказательство:
Пусть  - б.м.п. Тогда
- б.м.п. Тогда 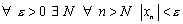 .
.
Возьмем  .
.
Тогда 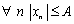 т.е.
т.е.  ограничена.
ограничена.
Следствие. Произведение б.м.п. есть также б.м.п.
4. Пусть  - б.м.п. и
- б.м.п. и  . Тогда
. Тогда  есть б.б.п.
есть б.б.п.
Доказательство:
 - б.м.п =>
- б.м.п => 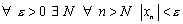 .
.
Возьмем любое  и положим
и положим 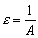 .
.
Тогда 
отсюда следует, что  есть б.б.п.
есть б.б.п.
5. Пусть  - б.б..п, тогда
- б.б..п, тогда  есть б.м.п.
есть б.м.п.
 - б.б.п =>
- б.б.п =>  .
.
Возьмем любое  и положим
и положим 
Тогда 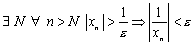 отсюда следует, что
отсюда следует, что  есть б.м.п.
есть б.м.п.
25. Вычисление предела:

Поиск по сайту: